Теорія кіс
Теорія кіс — розділ топології та алгебри, вивчає коси і групи кіс, складені з їхніх класів еквівалентності.
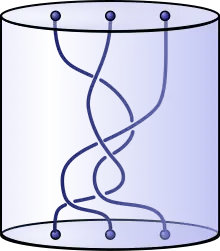
Визначення коси
Коса з ниток — об'єкт, що складається з двох паралельних площин і у тривимірному просторі , які містять упорядковані множини точок і і з роз'єднаних між собою простих дуг , які перетинають кожну паралельну площину між і одноразово і з'єднують точки з точками .
Зазвичай вважається, що точки лежать на прямій в , а точки на прямій в , паралельній , причому розташовані під для кожного .
Коси зображуються в проекції на площину, що проходить через і ця проекція може бути зведена в загальне положення так, що є лише скінченне число подвійних точок, попарно розташованих на різних рівнях, і перетини трансверсальні.
Група кіс
У множині всіх кіс з n нитками і з фіксованими вводиться відношення еквівалентності. Воно визначається гомеоморфізмами , де — область між і , тотожними на . Коси і еквівалентні, якщо існує такий гомеоморфізм , що .
Класи еквівалентності, далі також звані косами, утворюють групу кіс . Одинична коса — клас еквівалентності, який містить косу з n паралельних відрізків. Коса зворотна до коси , визначається відображенням у площині
Нитка коси з'єднує з і визначає підстановку, елемент симетричної групи . Якщо ця підстановка тотожна, то коса називається фарбованою (або чистою) косою. Це відображення задає епіморфізм на групу перестановок n елементів, ядром якого є підгрупа , яка відповідає всім чистим косам, так що є коротка точна послідовність
Сплетення
Нехай - тензорна категорія. Сплетенням у є структура комутування на , яка задовольняє двом співвідношенням:
для усіх об'єктів
Якщо - сплетення у , то й є сплетенням у .
Косовою моноїдальною категорією є моноїдальна категорія, оснащена сплетенням.
Нехай - векторний простір над Рівняння Янга-Бакстера - рівняння для лінійного автоморфізму з простору
Це рівняння є рівністю елементів групи автоморфізмів Його розв'язок називається -матрицею.
Для векторного простору через позначимо оператор перестановки співмножників, який представляє дві копії цього простору. Він визначається співвідношенням
Оператор перестановки задовольняє рівнянню Янга-Бакстера, оскільки в симетричній групі виконується співвідношення Кокстера[1]
де верхні індекси визначають транспозицію, яка міняє та
Нехай - асоціативна алгебра із одиницею (над деяким алгебрично замкненим полем нульової характеристики ), на якій визначена операція кодобутку задані антипод та косий антипод (тобто антипод для протилежного кодобутку ), а також одиниця є квазітрикутною супералгеброю Хопфа, якщо задовольняє квантовому рівнянню Янга-Бакстера:
а також співвідношенням[2]
Див. також
Література
- Сосинский А., Косы и узлы.[недоступне посилання з вересня 2019] Квант № 2, 1989, стор. 6-14 (рос.)
Посилання
- Christian Kassel, Marc Rosso, Vladimir Turaev - Quantum and knot invariants.
- Стукопин Владимир Алексеевич - Ангианы супералгебры Ли.
