Група кіс

Групу кіс уперше явно описав Еміль Артін 1925 року.[1]

Розглянемо випадок n = 4, з цього прикладу легко буде зрозуміти, що являє собою довільна група кіс. Розглянемо дві паралельні прямі (на малюнку вони розташовані вертикально), на кожній з яких лежить по чотири пронумеровані точки, так що точки з однаковими номерами знаходяться одна проти одної. Розіб'ємо точки на пари і за допомогою ниток з'єднаємо їх. Якщо зобразити картинку на площині, деякі нитки можуть під іншими (можна вважати, що нитки завжди перетинаються трансверсально). При цьому важливо враховувати порядок проходження ниток у точці перетину:

відрізняється від

З іншого боку, дві такі конфігурації, які можна зробити однаковими, переміщенням ниток, що не зачіпає кінцеві точки, ми вважатимемо однаковими:

не відрізняється від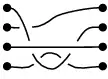

Всі нитки повинні бути напрямлені зліва направо, тобто кожна з ниток може перетинати вертикальну пряму (паралельну до прямих з пронумерованими точками) не більше ніж в одній точці:

не є косою.

Для двох кіс можна розглянути їх композицію, намалювавши другу поряд з першою, тобто склеївши відповідні чотири пари кінцевих точок:

×

=

Множину всіх кіс із 4 ниток позначають B₄. Описане з'єднання ниток є груповою операцією.

Група B₄ — це фактор-множина всіх таких конфігурацій на чотирьох парах точок за відношенням еквівалентності, заданим неперервними перетвореннями площини, на якому зазначеним вище способом задано групову операцію. Ця операція задовольняє всім аксіомам групи; зокрема, нейтральний елемент — клас еквівалентності чотирьох паралельних ниток і для кожного елемента обернений до нього можна отримати симетрією відносно вертикальної прямої.

Строго формалізувати наведений вище опис можна кількома способами:

• Геометричний спосіб використовує поняття гомотопії, а саме, B_n визначається як фундаментальна група простору n-точкових підмножин на площині з природною топологією.
• Також можна дати чисто алгебраичний опис, задавши твірні і співвідношення.
  • Наприклад, B_n можна задати (n − 1) твірною і ${\displaystyle {\tfrac {n\cdot (n-1)}{2}}}$ співвідношеннями:

    ${\displaystyle B_{n}=\langle \sigma _{1},\ldots ,\sigma _{n-1}\ \mid \ \sigma _{i}\sigma _{i+1}\sigma _{i}=\sigma _{i+1}\sigma _{i}\sigma _{i+1}\ {\text{при}}\ 1\leq i\leq n-2\ {\text{і}}\ \sigma _{i}\sigma _{j}=\sigma _{j}\sigma _{i}\ {\text{для}}\ |i-j|\geq 2\rangle$ :}

Зокрема, будь-який елемент B₄ можна записати як композицію таких трьох елементів (і обернених до них):

σ1	σ2	σ3

Щоб зрозуміти, чому це інтуїтивно очевидно, «проскануємо» картинку, переміщуючи вертикальну пряму зліва направо. Кожен раз, коли i-а зверху (на даній прямій) нитка проходить під (i + 1)-ю, будемо писати σ_i, а якщо над (i + 1)-ю, то σ_i⁻¹.

Очевидно, що виконується співвідношення σ₁σ₃ = σ₃σ₁, тоді як трохи складніше побачити, що σ₁σ₂σ₁ = σ₂σ₁σ₂ (переконатися в цьому найпростіше, намалювавши лінії на аркуші паперу).

Можна довести, що всі співвідношення між елементами групи кіс випливають зі співвідношень такого вигляду.

• Група B₁ тривіальна, B₂ нескінченна (як і всі наступні групи кіс) і ізоморфна Z, B₃ ізоморфна групі вузла трилисника.
• Всі елементи B_n, крім нейтрального, мають нескінченний порядок; тобто B_n не має кручення.
• Існує сюр'єктивний гомоморфізм B_n → S_n з групи кіс у групу перестановок. Дійсно, кожному елементу групи B_n можна зіставити перестановку множини n вершин, за якої лівому кінцю кожної «нитки» зіставляється правий її кінець.
  • Ядро цього гомоморфізму називається групою фарбованих кіс, вона зазвичай позначається ${\displaystyle P_{n}}$.
  • Для груп фарбованих кіс існує коротка точна послідовність

    ${\displaystyle F_{n-1}\to P_{n}\to P_{n-1},}$

  де ${\displaystyle F_{n-1}}$ позначає вільну групу з ${\displaystyle n-1}$ твірною.

• Групу кіс можна визначити як групу класів відображень диска з виколотими точками. Точніше, група кіс із n нитками природним чином ізоморфна групі класів перетворень диска n виколотими точками.

• Deligne, Pierre (1972). Les immeubles des groupes de tresses généralisés. Inventiones Mathematicae 17 (4): 273–302. ISSN 0020-9910. MR 0422673. doi:10.1007/BF01406236.
• Birman, Joan, and Brendle, Tara E., «Braids: A Survey», revised 26 February 2005. In Menasco and Thistlethwaite.
• Carlucci, Lorenzo; Dehornoy, Patrick; and Weiermann, Andreas, «Unprovability results involving braids», 23 November 2007
• Kassel, Christian; and Turaev, Vladimir, Braid Groups, Springer, 2008. ISBN 0-387-33841-1
• Menasco, W., and Thistlethwaite, M., (editors), Handbook of Knot Theory, Amsterdam: Elsevier, 2005. ISBN 0-444-51452-X

• CRAG: CRyptography and Groups на Algebraic Cryptography Center Містить велику бібліотеку для обчислень за допомогою груп кіс
• P. Fabel, Completing Artin's braid group on infinitely many strands, Journal of Knot Theory and its Ramifications, Vol. 14, No. 8 (2005) 979—991
• P. Fabel, The mapping class group of a disk with infinitely many holes, Journal of Knot Theory and its Ramifications, Vol. 15, No. 1 (2006) 21-29
• Chernavskii, A.V. (2001), «Braid theory», in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
• Java-застосунок, що моделює групу B₅.
• C. Nayak і F. Wilczek про зв'язок проективних груп кіс з дробовим квантовим ефектом Холла
• Презентація C. V. Nayak для FradkinFest
• Критика N. Read'ом реальності репрезентації Wilczek-Nayak