Теорія категорій

Теорія категорій — розділ математики, що вивчає властивості відношень між математичними структурами, незалежно від внутрішньої будови структур; абстрагується від множин та функцій до діаграм, де об'єкти сполучені морфізмами (стрілками).

Теорія категорій посідає центральне місце в сучасній математиці[1], а також має застосування в інформатиці[2] та теоретичній фізиці[3][4]. Сучасне викладання алгебраїчної геометрії та гомологічної алгебри основане на теорії категорії. Поняття теорії категорій використане в мові функційного програмування Haskell.

Історія

Поняття категорія було введено в 1945 році. Своїм походженням теорія категорій завдячує алгебраїчній топології. Подальші дослідження виявили об'єднувальну та уніфікувальну роль поняття категорія і пов'язаного з ним поняття функтора для багатьох розділів математики.

Теоретико-категорний аналіз основ теорії гомології привів до виділення у середині 50-х рр. 20 ст. так званих абелевих категорій, в рамках яких виявилося можливим здійснити основні побудови гомологічної алгебри. У 60-і рр. 20 ст. позначилася дедалі більша цікавість до неабелевих категорій, спонуканий задачами логіки, загальної алгебри, топології і алгебраїчної геометрії. Інтенсивний розвиток універсальної алгебри і аксіоматична побудова теорії гомотопій поклали початок різним напрямам досліджень: категорному дослідженню многовидів універсальної алгебри, теорії ізоморфізмів прямих розкладів, теорії зв'язаних функторів і теорії двоїстості функторів. Подальший розвиток виявив істотний взаємозв'язок між цими дослідженнями. Завдяки виникненню теорії відносних категорій, що широко використовує техніку зв'язаних функторів і замкнутих категорій, була встановлена двоїстість між теорією гомотопій і теорією універсальних алгебр, заснована на інтерпретації категорних визначень моноїда і комоноїда у відповідних функторів. Інший спосіб введення додаткових структур в категоріях пов'язаний із заданням в категоріях топології і побудові категорії пучків над топологічною категорією (так зв. топоси).

Визначення

Категорія

Категорія ${\mathcal {C}}$ складається з класу ${\text{Ob}}_{\mathcal {C}}$ , елементи якого називаються об'єктами категорії, та класу ${\text{Mor}}_{\mathcal {C}}$ , елементи якого називаються морфізмами категорії. Ці класи повинні задовольняти наступним умовам:

Кожній впорядкованій парі об'єктів А, В зіставлено клас ${\text{Hom}}_{\mathcal {C}}(A,B)$ ; якщо $f\in {\text{Hom}}_{\mathcal {C}}(A,B)$ , то А називається початком, або областю визначення морфізму f, а В — кінець, або область значень f.
Кожен морфізм категорії належить одному і лише одному класу ${\text{Hom}}_{\mathcal {C}}(A,B)$ .
У класі $Mor_{\mathcal {C}}$ заданий частковий закон множення: добуток морфізмів $f\in {\text{Hom}}(A,B)$ та $g\in {\text{Hom}}(C,D)$ визначено тоді і тільки тоді, коли В=С, він позначається $g\circ f$ і належить класу ${\text{Hom}}(A,D)$ .
Справедливий закон асоціативності: $h\circ (g\circ f)=(h\circ g)\circ f$ для будь-яких морфізмів, для яких дані добутки визначені.
У кожному класі ${\text{Hom}}(A,A)$ визначений такий морфізм $id_{A}$ , що $f\circ id_{A}=id_{B}\circ f=f$ для $f\in {\text{Hom}}(A,B)$ ; морфізми $id_{A}$ називаються одиничними, тотожними, або одиницями.

Замітка: клас об'єктів звичайно не є множиною в сенсі аксіоматичної теорії множин. Категорія, в якій об'єкти складають множину, називається малою. Крім того, у принципі можливо (з невеликим виправленням визначення) розглядати категорії, в яких морфізми між будь-якими двома об'єктами також утворюють клас, або навіть велику структуру[5].

Приклади категорій

Set — категорія множин. Об'єктами є множини, морфізмами — відображення множин, а множення збігається з послідовним виконанням відображень.
Top — категорія топологічних просторів. Об'єктами є топологічні простори, морфізмами — всі неперервні відображення топологічних просторів, а множення знову збігається з послідовним виконанням відображень.
Group — категорія груп. Об'єктами є групи, морфізмами — всі гомоморфізми груп, а множення збігається з послідовним виконанням гомоморфізмів. За аналогією можна ввести категорію кілець і т. д.
Vect_K — категорія векторних просторів над полем K. Морфізми — лінійні відображення векторних просторів.
Rel — категорія бінарних відношень множини; клас об'єктів цієї категорії збігається з класом об'єктів Set, а морфізмами множини А в множину В є бінарні відношення цих множин, тобто всілякі підмножини декартового добутку А×В; множення збігається з множенням бінарних відношень.
Моноїд є категорією з одним об'єктом, навпаки, кожна категорія, що складається з одного об'єкта, є моноїдом.
Для будь-якої частково впорядкованої множини можна побудувати малу категорію, об'єктами якої є елементи множини, причому між елементами x і y існує єдиний морфізм тоді і тільки тоді, коли x≤y (зрозуміло, слід відрізняти цю категорію від категорії частково впорядкованих множин).

Всі перераховані вище категорії допускають ізоморфне вкладення в категорію множин. Категорії з такою властивістю називаються конкретними. Не всяка категорія є конкретною, наприклад, категорія, об'єктами якої є всі топологічні простори, а морфізмами — класи гомотопних відображень.

Комутативні діаграми

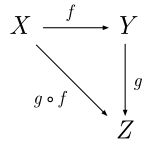
Категорія з об'єктами X, Y, Z та морфізмами f, g

Стандартним способом опису тверджень теорії категорій є комутативні діаграми. Комутативна діаграма — це орієнтований граф, у вершинах якого знаходяться об'єкти, а стрілками є морфізми або функтори, причому результат композиції стрілок не залежить від вибраного шляху. Наприклад, аксіоми теорії категорій можна записати за допомогою діаграм:

Двоїстість

Для категорії ${\mathcal {C}}$ можна визначити двоїсту категорію ${\mathcal {C}}^{op}$ , у якій:

об'єкти збігаються з об'єктами початкової категорії;
морфізми одержуються «обертанням стрілок»: ${\text{Hom}}_{{\mathcal {C}}^{op}}(B,A)\simeq {\text{Hom}}_{\mathcal {C}}(A,B)$

Взагалі, для будь-якого твердження теорії категорій можна сформулювати подвійне твердження за допомогою звернення стрілок. Часто подвійне явище позначається тим же терміном з приставкою ко- (див. приклади далі).

Справедливий принцип двоїстості: твердження р істинно в теорії категорій тоді і тільки тоді, коли в цій теорії істинно двоїсте твердження р^*. Багато понять і результатів в математиці виявилися двоїстими один одному з точки зору понять теорії категорій: ін'єктивність і сюр'єктивність, многовиди і радикали в алгебрі і т. д.

Морфізми

Морфізм $f\in {\text{Hom}}(A,B)$ називається ізоморфізмом, якщо існує такий морфізм $g\in {\text{Hom}}(B,A)$ , що $g\circ f=id_{A}$ та $f\circ g=id_{B}$ . Два об'єкти, між якими існує ізоморфізм, називаються ізоморфними. Зокрема, тотожний морфізм є ізоморфізмом, тому будь-який об'єкт ізоморфний сам собі.

Морфізми, в яких початок і кінець збігаються, називають ендоморфізмами. Множина ендоморфізмів $\ {\text{End}}(A)={\text{Hom}}(A,A)$ є моноїдом щодо операції композиції з одиничним елементом $\ id_{A}$ .

Ендоморфізми, які одночасно є ізоморфізмами, називаються автоморфізмами. Автоморфізми будь-якого об'єкта утворюють групу автоморфізмів $\ {\text{Aut}}(A)$ по композиції.

Мономорфізм — це морфізм $f\in {\text{Hom}}(A,B)$ такий, що для будь-яких $g_{1},g_{2}\in {\text{Hom}}(X,A)$ з $f\circ g_{1}=f\circ g_{2}$ випливає, що $\ g_{1}=g_{2}$ .

Композиція мономорфізмів є мономорфізмом.

Епіморфізм — це такий морфізм, що для будь-яких $g_{1},g_{2}\in {\text{Hom}}(B,X)$ з $g_{1}\circ f=g_{2}\circ f$ слідує $\ g_{1}=g_{2}$ .

Біморфізм — це морфізм, що є одночасно мономорфізмом і епіморфізмом. Будь-який ізоморфізм є біморфізмом, зворотне, взагалі кажучи, вірно не для всіх категорій.

Мономорфізм, епіморфізм і біморфізм є узагальненнями понять ін'єктивного, сюр'єктивного і бієктивного відображення відповідно.

Універсальні об'єкти

Початковий (універсально відштовхуючий) об'єкт категорії — це такий об'єкт, з якого існує єдиний морфізм в будь-який інший об'єкт.

Якщо початкові об'єкти в категорії існують, то всі вони ізоморфні.

Двоїстим чином визначається термінальний (універсально притягуючий) об'єкт — це такий об'єкт, в який існує єдиний морфізм з будь-якого іншого об'єкта.

Приклад: У категорії Set ініціальним об'єктом є порожня множина

\emptyset

, термінальним — множина з одного елементу

\{\cdot \}

.

Приклад: У категорії Group ініціальний і термінальний об'єкт збігаються — це група з одного елементу.

Добуток і сума об'єктів

добуток

кодобуток (пряма сума)

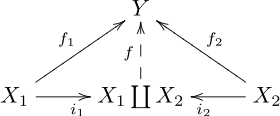
Добуток об'єктів $X_{1}$ та $X_{2}$ — це об'єкт $X_{1}\times X_{2}$ з морфізмами $\pi _{1}:X_{1}\times X_{2}\to X_{1}$ та $\pi _{2}:X_{1}\times X_{2}\to X_{2}$ такими, що для будь-якого об'єкта $Y$ з морфізмами $f_{1}:Y\to X_{1}$ та $f_{2}:Y\to X_{2}$ існує єдиний морфізм $f:Y\to X_{1}\times X_{2}$ такий, що $f\circ \pi _{1}=f_{1},\quad f\circ \pi _{2}=f_{2}$ .

Морфізми $\pi _{1}:X_{1}\times X_{2}\to X_{1}$ та $\pi _{2}:X_{1}\times X_{2}\to X_{2}$ називаються проекціями.

Дуально визначається кодобуток (пряма сума): $X_{1}+X_{2}$ об'єктів $X_{1}$ і $X_{2}$ . Відповідні морфізми $i_{1}:X_{1}\to X_{1}+X_{2}$ та $i_{2}:X_{2}\to X_{1}+X_{2}$ називаються вкладеннями. Не зважаючи на свою назву, в загальному випадку вони можуть і не бути мономорфізмами.

Якщо добуток і кодобуток існують, то вони визначаються однозначно з точністю до ізоморфізму.

Приклади

У категорії Set прямий добуток A і B — це добуток в сенсі теорії множин $A\times B$ , а пряма сума — диз'юнктне об'єднання $A\sqcup B$ .
У категорії Ring пряма сума — це тензорний добуток $A\otimes B$ , а прямий добуток — сума кілець $A\oplus B$ .
У категорії Vect_K прямий добуток і пряма сума ізоморфні — це сума векторних просторів $A\oplus B$ .

Фактор-категорія

Фактор-категорія — конструкція, яка є аналогічною конструкції фактор-множини або фактор-алгебри. Нехай $R$ — довільна категорія, у класі морфізмів $\mathrm {Mor} \,R$ задане відношення еквівалентності $\sim ,$ яке задовільняє наступним умовам

якщо $\alpha \sim \beta ,$ то кінці морфізмів $\alpha$ та $\beta$ співпадають;
якщо $\alpha \sim \beta ,\,\,\gamma \sim \delta$ та добуток $\alpha \gamma$ визначений, то $\alpha \gamma \sim \beta \delta .$

Через $[\alpha ]$ позначається клас еквівалентності морфізму $\alpha .$ Фактор-категорією категорії ${\mathcal {R}}$ по відношенню еквівалентності називається категорія ${\mathcal {R}}/\sim ,$ у якої ті самі об'єкти, що й у ${\mathcal {R}},$ а для будь-якої пари об'єктів $A,B$ множина морфізмів $\mathrm {Mor} (A,B)\in {\mathcal {R}}/\sim$ складається з класів еквівалентності $[\alpha ],$ де $\alpha :A\rightarrow B$ у $R;$ добуток морфізмів $[\alpha ],[\beta ]$ визначається формулою $[\alpha ][\beta ]=[\alpha \beta ].$

Усяка мала категорія є фактор-категорії шляхів над підходячим орієнтованим графом.[6]

Ядерна пара морфізму — узагальнення поняття еквівалентности, індукованого відображенням однієї множини у іншу. Морфізми $\vartheta _{1},\vartheta _{2}:R\rightarrow A$ категорії ${\mathcal {R}}$ є ядерною парою морфізму $\alpha :A\rightarrow B,$ якщо $\vartheta _{1}\alpha =\vartheta _{2}\alpha$ та якщо для пари довільних морфізмів $\varphi ,\psi :X\rightarrow A,$ для якої $\varphi \alpha =\psi \alpha ,$ існує такий єдиний морфізм $\gamma :X\rightarrow R,$ що $\varphi =\gamma \vartheta _{1}$ та $\psi =\gamma \vartheta _{2}.$

Функтори

Функтори — відображення категорій, що зберігають структуру. Точніше

(Коваріантний) функтор ${\mathcal {F}}:{\mathcal {C}}\to {\mathcal {D}}$ $\text{[math]}$ ставить у відповідність кожному об'єктові категорії ${\mathcal {C}}$ $\text{[math]}$ об'єкт категорії ${\mathcal {D}}$ $\text{[math]}$ і кожному морфізму $f:A\to B$ $\text{[math]}$ морфізм $F(f):F(A)\to F(B)$ $\text{[math]}$ так, що
- $F(id_{A})=id_{F(A)}\,$ і
- $F(g)\circ F(f)=F(g\circ f)$ .

Контраваріантний функтор, або кофунктор — це функтор з ${\mathcal {C}}$ у ${\mathcal {D}}^{op}$ , тобто «функтор, що перевертає стрілки».

Мала категорія

Клас об'єктів не обов'язково є множиною у сенсі аксіоматичної теорії множин. Категорія ${\mathcal {C}}$ , у якій об'єкти $\mathrm {Ob} \,{\mathcal {C}}$ є множиною та морфізми $Mor({\mathcal {C}})$ є множиною, називається малою.

Нехай ${\mathcal {F}}:\mathbb {C} \rightarrow \mathbb {D}$ — функтор з малої категорії у довільну. Шаром ${\mathcal {F}}/d$ функтора ${\mathcal {F}}$ над $a\in \mathrm {Ob} \,\mathbb {D}$ є категорія, об'єктами якої є пари $(a,\alpha )$ об'єктів $a\in \mathrm {Ob} \,\mathbb {C}$ та морфізмів $\alpha :Sa\rightarrow d$ категорії $\mathbb {D}$ , а морфізмами $(a,\alpha )\rightarrow (b,\beta )$ між парами — трійки $(f,\alpha ,\beta )$ морфізмів $f\in \mathbb {C} (a,b),\,\,a\in \mathbb {D} (Sa,d),\,\,\beta \in \mathbb {D} (Sb,\,\beta )$ таких, що $\beta \circ Sf=\alpha .$ Двоїсто, ко-шаром $d/S$ називається категорія, яка складається з пар $(a,\alpha )$ об'єктів $a\in \mathrm {Ob} \,\mathbb {C}$ та морфізмів $\alpha :d\rightarrow Sa,$ у якій морфізмами $(a,\alpha )\rightarrow (b,\beta )$ є трійки $(f,a\rightarrow b,\alpha ,\beta ),$ які задовільняють співвідношенню $Sf\circ \alpha =\beta .$ Функтор ${\mathcal {H}}_{d}:d/S\rightarrow \mathbb {C}$ (або, відповідно, ${\mathcal {H}}_{d}:S/d\rightarrow \mathbb {C}$ ), який діє як $(a,\alpha )\mapsto a$ на об'єктах й як $(f,\alpha ,\beta )\mapsto f$ на морфізмах, називається забуваючим функтором.

Тензорна категорія

Нехай ${\mathcal {C}}$ категорія та нехай ${\displaystyle \otimes$ — функтор, які називаються тензорним добутком. Категорія називається тензорною, якщо виконуються наступні умови:

Заданий деякий ізоморфізм функторів $a:\otimes (\otimes \times 1)\rightarrow (1\times \otimes ).$ Це значить, що для $U,V,W,X\in {\mathcal {C}}$ є ізоморфізм.
Виконується аксіома п'ятикутника: $\forall \,\,U,V,W,X\in {\mathcal {C}}\quad \quad a_{U,V,W\otimes X}\circ a_{U\otimes V,W,X}=(1_{U}\otimes a_{V,W,X})\circ a_{U,V\otimes W,X}\circ a_{U,V,W\otimes 1_{X}}.$
Є об'єкт $I,$ для якого задані натуральні ізоморфізми $l:\otimes (I\times 1)\rightarrow 1$ та $r:\otimes (1\times I)\rightarrow 1.$
Виконується аксіома трикутника:

$V,W\in {\mathcal {C}}\quad \quad (1_{V}\otimes l_{W})\circ a_{V,I,W}=r_{V}\otimes 1_{W}.$

Наприклад, для трійок $U,V,W\in {\mathcal {C}}$ та $f,g,h\in \mathrm {Mor_{\mathcal {C}}}$ є такий ізоморфізм $a_{U,V,W}:(U\otimes V)\otimes W\rightarrow U\otimes (V\otimes W)$ , що діаграма

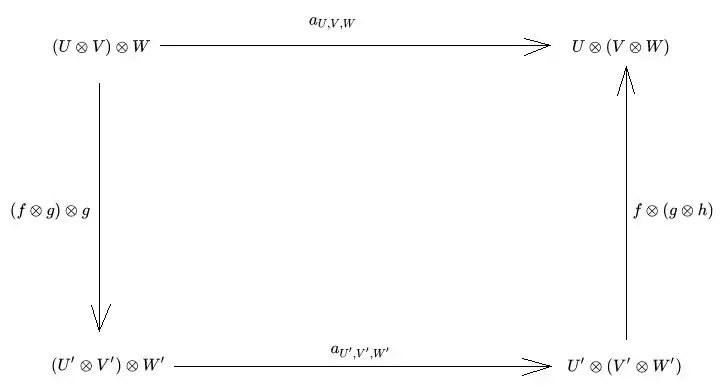
є комутативною.[7]

Категорія Дрінфельда

Володимир Гершонович Дрінфельд визначив квазі-трикутну моноїдальну категорію. Нехай ${\mathfrak {C}}$ — категорія, об'єктами якої є ${\mathfrak {g}}$ -модулі, а $\mathrm {Hom} _{\mathfrak {C}}(U,W)=\mathrm {Hom} _{\mathfrak {g}}(U,W)[[n]].$ Це — $C$ -лінійна адитивна категорія. Тепер нехай $V_{1},V_{2},V_{3}\in {\mathfrak {C}}.$ Розгляньмо гомоморфізм $\theta :T_{3}[[\hbar ]]\rightarrow End(V_{1}\otimes V_{2}\otimes V_{3}),$ який визначається формулою $\theta (t_{ij}=\Omega _{ij})$ , і $\Phi _{V_{1}V_{2}V_{3}}=\theta (\Phi ).$ Тут $\Phi$ є морфізмом асоціативності (асоціатором Дрінфельда). Через $\Omega$ позначений елемент Казіміра. Через $T_{3}[[\hbar ]]$ позначені співвідношення шестикутника. Для довільних $V_{1},V_{2}\in {\mathfrak {C}}$ має місце тензорний добуток $V_{1}\otimes V_{2}.$ Морфізм асоціативності $\Phi _{V_{1}V_{2}V_{3}}$ є елементом $\mathrm {Hom} _{\mathfrak {C}}((V_{1}\otimes V_{2})\otimes V_{3},\,\,V_{1}\otimes (V_{2}\otimes V_{3})).$ Для $V_{1},V_{2}\in {\mathfrak {C}}$ визначмо також скручення ${\mathfrak {S}}_{V_{1}V_{2}}:V_{1}\otimes V_{2}\rightarrow V_{2}\otimes V_{1}$ формулою ${\mathfrak {S}}_{V_{1}V_{2}}=s\circ \exp(\hbar \Omega /2),$ де $s$ є перестановкою. Морфізми $\Phi _{V_{1}V_{2}V_{3}},\,\,{\mathfrak {S}}_{V_{1}V_{2}}$ визначають структуру квазі-трикутної категорії на ${\mathfrak {S}}.$ [8]

Функтор Сера

Функтором Сера триангульованої $C$ -лінійної $\mathrm {Hom}$ -скінченної категорії ${\mathcal {A}}$ є коваріантний адитивний функтор $F:{\mathcal {A}}\rightarrow {\mathcal {A}},$ який комутує із зсувами, якщо має місце автоеквівалентність $F:{\mathcal {A}}\rightarrow {\mathcal {A}}$ така, що мають місце біфункторіальні ізоморфізми

$\mathrm {Hom} _{\mathcal {A}}(E,G)\cong D\mathrm {Hom} _{\mathcal {A}}(G,F(E)),$

де $D=\mathrm {Hom} _{C}(-,k),\,\,\,E,G\in \mathrm {Ob} \,{\mathcal {A}}.$ Якщо функтор Сера існує, то він єдиний з точністю до ізоморфізму.

Для гладкого проективного многовиду $M$ розмірності $n$ й канонічного пучка $\omega _{M}=\land ^{n}\Omega _{M}$ класична двоїстість Сера

$H^{i}(M,{\mathfrak {F}})\cong D\,\,\mathrm {Ext} ^{n-i}({\mathfrak {F}},\omega _{M}),$

де ${\mathfrak {F}}\in \mathrm {coh} (M),$ є наслідком того, що $F=-\otimes \omega _{M}[n]$ є функтором Сера на довільній категорії обмежених комплексів когерентних пучків $D^{b}(\mathrm {coh} (M)).$ Якщо на триангульованій $C$ -лінійній $\mathrm {Hom}$ -скінченній категорії ${\mathcal {A}}$ є функтор Сера, то така категорія є категорією із двоїстістю Сера.

Нехай $A$ — скінченновимірна алгебра над $C,$ яка має скінченну гомологічну розмірність, ${\mathcal {A}}=D^{b}(A-\mathrm {mod} )$ — довільна категорія скінченновимірних лівих $A$ -модулів. Наявні два функтори дуалізації, які переводять $D^{b}(A-\mathrm {mod} )$ у $D^{b}(\mathrm {mor} -A)$ (праві моулі), й навпаки:

$D^{b}(A-\mathrm {mod} ){\overset {\delta }{\rightarrow }}D^{b}(\mathrm {mod} -A){\overset {d}{\rightarrow }}D^{b}(A-\mathrm {mod} ),$

$\delta (M^{*})=R\,\,\mathrm {Hom} _{A}(M^{*},A);\quad \quad d(M^{*})=\mathrm {Hom} _{C}(M^{*},C).$

Тут $\mathrm {mod} -A$ — категорія скінченнопороджених модулів над скінченновимірною $C$ -алгеброю $A$ глобальної розмірності. Композиція $F=d\circ \delta$ називається функтором Накаями й є функтором Сера у категорії ${\mathcal {A}}=D^{b}(A-\mathrm {mod} ).$

Тріагнульована $C$ -лінійна $\mathrm {Hom}$ -скінченна категорія ${\mathcal {A}}$ називається категорією Калабі-Яу, якщо триангульований $n$ -кратний функтор зсуву $[n]$ є функтором Сера. Найменше $n\geq 0$ називається розмірністю Калабі-Яу категорії ${\mathcal {A}}$ й позначається $\mathrm {CYdim} ({\mathcal {A}}).$ Якщо категорія ${\mathcal {A}}$ не є категорією Калабі-Яу, то $\mathrm {CYdim} ({\mathcal {A}})=\infty .$

Триангульовані категорії із двоїстістю Сера представляють інтерес тому, що на спадкових абелевих категоріях $\mathbb {A}$ Нетер є двоїстість Сера.[9]

Мультикатегорія

Мультикатегорією є набір об'єктів $a,b,...,$ стрілок $f_{1},f_{2},...,$ операція композиції визначається як у звичайній категорії. У звичайній категорії область визначення $\mathrm {dom\,} f$ — одиничний об'єкт, тоді як у мультикатегорії це скінченна множина об'єктів. Іншими словами, для звичайної категорії $a\rightarrow b,$ тоді як у мультикатегорії ${\begin{bmatrix}a_{1}\\a_{2}\\...\\a_{k}\end{bmatrix}}\rightarrow b,\quad k\in \mathbb {N} .$

Примітки

Хелемский А. Я. Лекції по функціональному аналізу. — М.:МЦНМО, 2004 ISBN 5-94057-065-8
D.E. Rydeheard, R.M. Burstall Computational Category Theory, — New York: Prentice Hall. — в 1988. — XIII, 257 р. — ISBN 0-13-162736-8.
Чи потрібна фізикам теорія категорій?
Топоси для фізики. Архівовано 5 грудня 2008 у Wayback Machine. {ref-en}
J. Adámek, H. Herrlich, G. E. Strecker Abstract and concrete categories: The joy of cats, — New York: John Wiley and Sons, — 1990.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
Тензорные категории и R - матрица для Uq(sl2).
В. Г. Дринфельд, О квазитреугольных квазихопфовых алгебрах и одной группе, тесно связанной с Gal(Q/Q), Алгебра и анализ, 1990, том 2, выпуск 4, 149–181.
А. И. Бондал, М. М. Капранов, Представимые функторы, функторы Серра и перестройки, Изв. АН СССР. Сер. матем., 1989, том 53, выпуск 6, 1183–1205.

Див. також

Література

С. Маклейн Категории для работающего математика, — М.: ФИЗМАТЛИТ, 2004. — 352 с — ISBN 5-9221-0400-4.
И. Букур, А. Деляну Введение в теорию категорий и функторов. — М.: Мир, 1972.
Цаленко М. С., Шульгейфер Е. Г. Основы теории категорий. — М.: Наука, 1974.
Adámek, Jiří; Herrlich, Horst; Strecker, George E. (1990). Abstract and concrete categories. John Wiley & Sons. ISBN 0-471-60922-6.
Awodey, Steven (2006). Category Theory (Oxford Logic Guides 49). Oxford University Press.
Pedicchio, Maria Cristina; Tholen, Walter (2004). Categorical foundations. Encyclopedia of Mathematics and its Applications 97. Cambridge University Press.

Посилання

Категорій теорія // Енциклопедія сучасної України : у 30 т. / ред. кол. І. М. Дзюба [та ін.] ; НАН України, НТШ. — К. : Інститут енциклопедичних досліджень НАН України, 2001–2020. — ISBN 944-02-3354-X.
Category Theory and Haskell
Category Theory for Programmers

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Хелемский А. Я. Лекції по функціональному аналізу. — М.:МЦНМО, 2004 ISBN 5-94057-065-8

[2] D.E. Rydeheard, R.M. Burstall Computational Category Theory, — New York: Prentice Hall. — в 1988. — XIII, 257 р. — ISBN 0-13-162736-8.

[3] Чи потрібна фізикам теорія категорій?

[4] Топоси для фізики. Архівовано 5 грудня 2008 у Wayback Machine. {ref-en}

[JoyOfCats-5] J. Adámek, H. Herrlich, G. E. Strecker Abstract and concrete categories: The joy of cats, — New York: John Wiley and Sons, — 1990.

[6] Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.

[7] Тензорные категории и R - матрица для Uq(sl2).

[8] В. Г. Дринфельд, О квазитреугольных квазихопфовых алгебрах и одной группе, тесно связанной с Gal(Q/Q), Алгебра и анализ, 1990, том 2, выпуск 4, 149–181.

[9] А. И. Бондал, М. М. Капранов, Представимые функторы, функторы Серра и перестройки, Изв. АН СССР. Сер. матем., 1989, том 53, выпуск 6, 1183–1205.