Трисекція кута

Нехай нам треба поділити кут α на 3 рівні частини. Зробимо це з допомогою комплексних чисел.

Трисекція кута з допомогою комплексних чисел

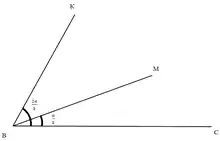
Щоб знайти координати К, піднесемо

${\displaystyle (0+i)^{\frac {\alpha }{90}}={\sqrt[{90}]{(0+i)^{\alpha }}}=1(\cos({\frac {\alpha {\frac {\pi }{2}}+2\pi k}{90}})+isin({\frac {\alpha {\frac {\pi }{2}}+2\pi k}{90}}))}$

При k = 0:

${\displaystyle (0+i)^{\frac {\alpha }{90}}=1(\cos({\frac {\alpha {\frac {\pi }{2}}}{90}})+isin({\frac {\alpha {\frac {\pi }{2}}}{90}}))=\sin(\alpha )+\cos(\alpha )}$

Щоб знайти координати точки L, піднесемо:

${\displaystyle ({\frac {\sqrt {3}}{2}}+{\frac {1}{2}}i)^{\frac {\alpha }{90}}={\sqrt[{90}]{({\frac {\sqrt {3}}{2}}+{\frac {1}{2}}i)^{\alpha }}}=1(\cos({\frac {\alpha {\frac {\pi }{6}}+2\pi k}{90}})+isin({\frac {\alpha {\frac {\pi }{6}}+2\pi k}{90}}))}$

При k = 0:

${\displaystyle ({\frac {\sqrt {3}}{2}}+{\frac {1}{2}}i)^{\frac {\alpha }{90}}=1(\cos({\frac {\alpha {\frac {\pi }{6}}}{90}})+isin({\frac {\alpha {\frac {\pi }{6}}}{90}}))=(\cos({\frac {\alpha }{3}})+i\sin({\frac {\alpha }{3}}))}$

Щоб знайти координати точки M, піднесемо:

${\displaystyle ({\frac {1}{2}}+{\frac {\sqrt {3}}{2}}i)^{\frac {\alpha }{90}}={\sqrt[{90}]{({\frac {1}{2}}+{\frac {\sqrt {3}}{2}}i)^{\alpha }}}=1(\cos({\frac {\alpha {\frac {\pi }{3}}+2\pi k}{90}})+isin({\frac {\alpha {\frac {\pi }{3}}+2\pi k}{90}}))}$

При k = 0:

${\displaystyle ({\frac {1}{2}}+{\frac {\sqrt {3}}{2}}i)^{\frac {\alpha }{90}}=1(\cos({\frac {\alpha {\frac {\pi }{6}}}{90}})+isin({\frac {\alpha {\frac {\pi }{6}}}{90}}))=(\cos({\frac {\alpha }{3}})+i\sin({\frac {\alpha }{3}}))}$

Очевидно, що ${\displaystyle 0+0i}$ i ${\displaystyle 1+0i}$ при піднесенні до будь-якого степеня завжди буде незмінним. Бачимо, що:

${\displaystyle \angle KBC=\alpha ,\angle LBC={\frac {\alpha }{3}},\angle MBC={\frac {\alpha }{3}}}$

Отже, ми поділили кут на 3 рівні частини

Трисекція кута за допомогою плаского оріґамі

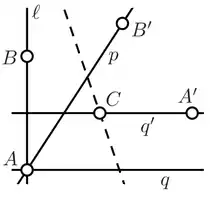
Нехай кут заданий двома складками p і q, позначимо через А вершину кута. Спочатку проведем підготовчі побудови, використаєм властивість оріґамі, яка каже, що лист можна скласти

так, що дві відмічені точки будуть на складці. Далі використаємо іншу властивість, лист можна скласти так, що відмічена точка попаде на складку, а відмічена пряма перейде в себе

(тобто, лінія складки буде їй перпендикулярна), таким чином відновим перпендикуляр l до q, через А і використовуючи ще одну властивість, лист можна скласти так, що одна відмічена

точка перейде в другу відмічену точку, відмітим на l будь-яку точку В і відновим серединний перпендикуляр q` до відрізка АВ через ту саму властивість.

Тепер складемо лист так, щоб А попала на q`, а В на p, використовуючи властивість про те, що лист, який має  дві відмічені прямі p і q і дві точки А і В, можна скласти так, що точка А попаде

на пряму р, а точка В на пряму q. При цьому образ А` вершини А ляже на першу трисектрису  нашого кута, а точка С на перетин q` з новою складкою  буде лежати на другій. Тобто промені

АА` і АС будуть ділити кут на три рівні частини.

Трисекція кута за допомогою равлика Паскаля

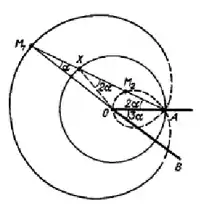
Візьмемо на окружності радіуса R точку А і проведемо через неї пряму l. Пряма l пересікає окружність в точках Х і А, якщо l дотична, то Х = А. Нехай М1 і М2 – такі точки прямої l, що ХМ1 = ХМ2 = а, де а – константа. Множина точок М1 і М2 (для всіх прямих l) називають равликом Паскаля. Нас буде цікавити випадок коли а = R. Нехай вектори ХМ1  і АХ співнапрямлені, В – точка на продовжені відрізка  М1О за точку О. Так як трикутники ∠М1ХО і ∠ХОА рівнобедрені, то ∠ОАХ = 2∠ОМ1А і ∠АОВ =  ∠ОМ1А + ∠ОАХ = 3∠ОМ1А. Тому для трисекції ${\displaystyle \angle \varphi }$, де  ${\displaystyle 0<\varphi <\pi /2}$, можна поступити наступним чином. Візьмемо точку В так, що ∠АОВ = ∠${\displaystyle \varphi }$. Нехай пряма ОВ перетинає суцільну частину равлика Паскаля в точці М1 (пунктирна частина равлика Паскаля відповідає таким точкам М2, що вектори Х М1 і АХ різнонапрямлені). Тоді ∠ОМ1А = ∠${\displaystyle \varphi /3}$.

Нехай треба випадково взятий гострий ∠ABC розділити на три рівні частини. Для цього із вершини даного кута B, як з центра, випадковим радіусом R опишемо коло. Точки перетину сторін даного кута з колом позначимо як D і F. Тепер візьмемо невсіса F і G, причому довжина відрізка FG - R, і прикладаємо його до точки R так, щоб F і G виявились на одній прямій з точкою E і щоб F знаходилась на колі, а G - на продовжені сторони BA Тоді ∠EGD і буде являтись однією третьою заданого ∠ABC.

Трисекція за допомогою невсіса

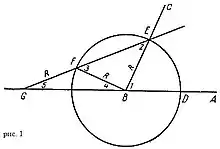
Доведемо це. Позначимо для краси кути на рисунку цифрами 1,2,3,4,5. Треба довести, що кут 5 є третьою частиною кута 1, тобто ${\displaystyle \angle 5={\frac {1}{3}}\angle 1}$.

Насправді, за властивістю зовнішнього кута трикутника, ${\displaystyle \angle 1=\angle 2+\angle 5}$, але, за властивістю зовнішнього трикутника, ${\displaystyle \angle 3=\angle 5+\angle 4}$. Далі, за властивістю рівнобедриного трикутника, ${\displaystyle \angle 5=\angle 4}$. Тоді ${\displaystyle \angle 3=2\angle 5}$. Із трикутника BFF, оскільки він рівнобедрений, ${\displaystyle \angle 3=\angle 2}$. Враховуючи попередні рівності, маємо: ${\displaystyle \angle 1=\angle 5+\angle 3=\angle 5+2\angle 5=3\angle 5}$

Значить, ${\displaystyle \angle 5={\frac {1}{3}}\angle 1}$, що і треба було довести.