Равлик Паскаля

Равлик Паскаля ― пласка алгебрична крива 4-го порядку; подера кола, конхоїда кола відносно точки на колі, частковий випадок декартового овалу, вона також є епітрохоїдою. Названа за ім'ям Етьєна Паскаля (батька Блеза Паскаля), який вперше розглянув її.

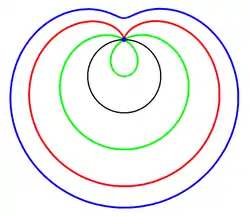
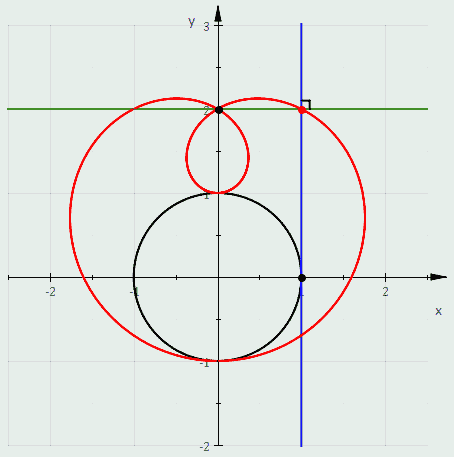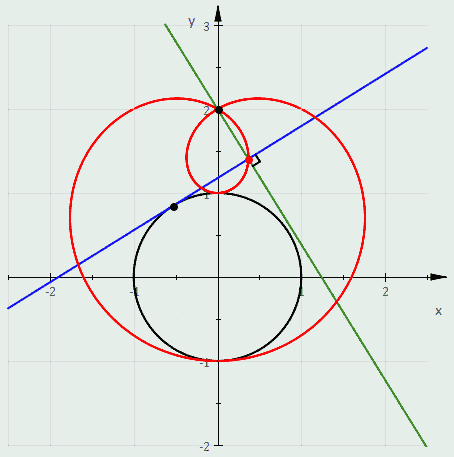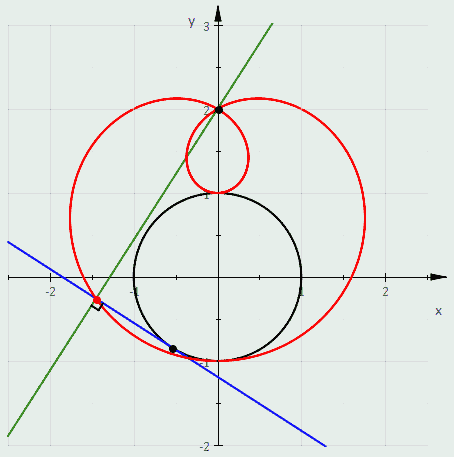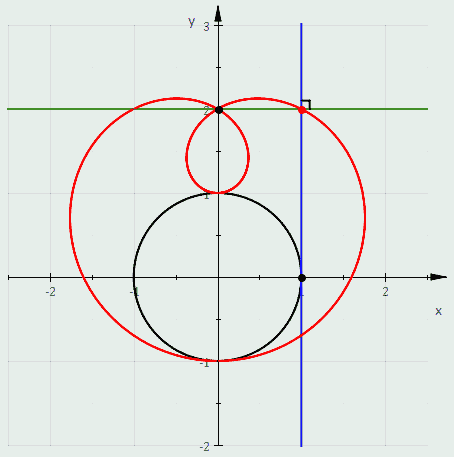
Три равлики Паскаля, конхоїди чорного кола: зелена

a>\ell

, червона (кардіоїда)

a=\ell

і синя

a<\ell

Рівняння

(x^{2}+y^{2}-ay)^{2}=\ell ^{2}(x^{2}+y^{2})

\rho =\ell -a\sin \phi .

Тут a — діаметр вихідного кола, а l — відстань, на яку зміщається точка вздовж радіус-вектора (див. конхоїда).

Звичайне:

{\displaystyle {\begin{cases}x=a\cos ^{2}\phi +\ell \cos \phi

Раціональне $(u=\tan {\frac {\phi }{2}})$ :

{\begin{cases}x={\frac {1-u^{2}}{(1+u^{2})^{2}}}((\ell +a)+u^{2}(\ell -a));\\y={\frac {2u}{(1+u^{2})^{2}}}((\ell +a)+u^{2}(\ell -a));\end{cases}}

Початок координат є
- вузловою точкою при $a>\ell$ .
- точкою повернення при $a=\ell$ (у цьому випадку равлик Паскаля називається кардіоїдою).
- подвійною точкою, ізольованою при $a<\ell$ .
Довжина дуги виражається еліптичним інтегралом 2-го роду.
Площа, обмежена равликом Паскаля:
$S={\frac {\pi a^{2}}{2}}+\pi \ell ^{2}$ ;
при $a>\ell$ площа внутрішньої петлі при обчисленні за цією формулою враховується двічі.
У разі $\ell =2a$ , равлик Паскаля також називається трисектрисою. Таку назву він отримав через те, що, якщо на площині задано трисектрису, то трисекцію кута можна побудувати за допомогою циркуля і лінійки.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.