Функція Гудермана
Функція Гудермана(також гіперболічна амплітуда або гудерманіан) — спеціальна функція, що пов'язує тригонометричні і гіперболічні функції. Названа на честь німецького математика Крістофа Гудермана.
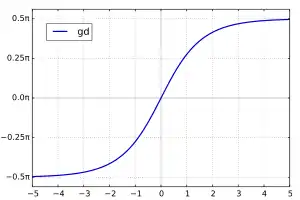
Функція визначена як:
Головні властивості
Функція Гудермана визначає зв'язок, який існує між тригонометричними і гіперболічними функціями без застосування комплексного аналізу.
Експоненційну функцію можна виразити через функцію Гудермана:
Похідна функції Гудермана рівна:
Розклад в ряд Тейлора для функції Гудермана має вигляд:
Обернена функція
Обернена функція до функції Гудермана (що позначається як або ) рівна:
Окрім того справедливою є рівність:
Похідна оберненої функції Гудермана рівна:
Похідні, ряди, інтеграли
Производні функції Гудермана і оберненої функції Гудермана дорівнюють відповідно гіперболічному і тригонометричному секансу:
Розклад у ряд:
Коефіцієнти розкладу гудерманіана і антигудерманіана при членах однакового степеня збігаються за модулем, однак у членів зі степенями 3, 7, 11,... коефіцієнти розкладу гудерманіана від'ємні, а в оберненої функції — додатні.
Інтеграл функції Гудермана:
где Li2 — дилогарифм.
Гудерманіан і антігудерманіан, що дозволяють легко переходити від гіперболічних до тригонометричних функцій і назад, використовуються для аналітичного інтегрування методом тригонометричної і гіперболічної підстановки.
Див. також
Посилання
- Weisstein, Eric W. Функція Гудермана(англ.) на сайті Wolfram MathWorld.
