Функція Ейрі

Для дійсних x, функція Ейрі та функція Ейрі другого роду визначаються інтегралом:

${\displaystyle \mathrm {Ai} (x)={\frac {1}{\pi }}\int \limits _{0}^{\infty }\cos \left({\frac {t^{3}}{3}}+xt\right)\,dt.}$

${\displaystyle \mathrm {Bi} (x)={\frac {1}{\pi }}\int \limits _{0}^{\infty }\exp \left(-{\frac {t^{3}}{3}}+xt\right)+\sin \left({\frac {t^{3}}{3}}+xt\right)\,dt.}$

Виконуючи диференціювання під знаком інтегралу, можна переконатися, що ці функції справді задовольняють рівнянню Ейрі.

${\displaystyle y''-xy=0\,.}$

При ${\displaystyle x\rightarrow -\infty }$ функція Ейрі другого роду має однакову амплітуду коливань із функцією Ейрі, які, проте, відрізняються протилежною фазою.

В точці x=0 функції Ai(x) і Bi(x) та їх похідні мають значення

${\displaystyle {\begin{aligned}\mathrm {Ai} (0)&{}={\frac {1}{3^{2/3}\Gamma ({\frac {2}{3}})}},&\quad \mathrm {Ai} '(0)&{}=-{\frac {1}{3^{1/3}\Gamma ({\frac {1}{3}})}},\\\mathrm {Bi} (0)&{}={\frac {1}{3^{1/6}\Gamma ({\frac {2}{3}})}},&\quad \mathrm {Bi} '(0)&{}={\frac {3^{1/6}}{\Gamma ({\frac {1}{3}})}}.\end{aligned}}}$

де ${\displaystyle \Gamma (x)}$ — гамма-функція. Звідси випливає, що визначник Вронського функцій Ai(x) та Bi(x) дорівнює 1/π.

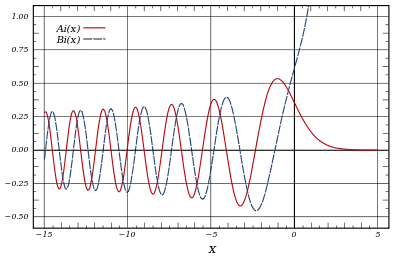
При додатних x Ai(x) — додатна, опукла функція, яка зменшується експоненційно до 0, а Bi(x) — додатна опукла функція, котра зростає експоненційно. При від'ємних x Ai(x) та Bi(x) коливається навколо нуля із дедалі більшою частотою й дедалі меншою амплітудою. Це підтверджується асимптотичними виразами для функцій Ейрі.

При ${\displaystyle x\rightarrow \infty }$:

${\displaystyle {\begin{aligned}\mathrm {Ai} (x)&{}\sim {\frac {e^{-{\frac {2}{3}}x^{3/2}}}{2{\sqrt {\pi }}\,x^{1/4}}}\\\mathrm {Bi} (x)&{}\sim {\frac {e^{{\frac {2}{3}}x^{3/2}}}{{\sqrt {\pi }}\,x^{1/4}}}.\end{aligned}}}$

При ${\displaystyle x\rightarrow -\infty }$ :

${\displaystyle {\begin{aligned}\mathrm {Ai} (-x)&{}\sim {\frac {\sin({\frac {2}{3}}x^{3/2}+{\frac {1}{4}}\pi )}{{\sqrt {\pi }}\,x^{1/4}}}\\\mathrm {Bi} (-x)&{}\sim {\frac {\cos({\frac {2}{3}}x^{3/2}+{\frac {1}{4}}\pi )}{{\sqrt {\pi }}\,x^{1/4}}}.\end{aligned}}}$

Функція Ейрі може бути аналітично продовжена на комплексну площину за формулою

${\displaystyle \mathrm {Ai} (z)={\frac {1}{2\pi i}}\int \limits _{C}\exp \left({\frac {t^{3}}{3}}-zt\right)\,dt,}$

де інтеграл береться по контуру ${\displaystyle C}$, котрий починається в точці на нескінченності із аргументом −π/3 і закінчується в точці на нескінченності із аргументом π/3. Можна підійти з іншого боку, використовуючи диференціальне рівняння ${\displaystyle y''-xy=0}$ для продовження Ai(x) та Bi(x) до цілих функцій на комплексній площині.

Асимптотична формула для Ai(x) залишається в силі на комплексній площині, якщо брати головне значення кореня x^2/3 і x не лежить на від'ємній дійсній півосі. Формула для Bi(x) правильна, якщо x лежить в секторі {x∈C : |arg x| < (1/3)π−δ} для деякого додатного δ. Формули для Ai(−x) та Bi(−x) справедливі, якщо x лежить в секторі {x∈C : |arg x| < (2/3)π−δ}.

Із асимптотичної поведінки функцій Ейрі витікає, що обидві вони мають нескінченне число нулів (коренів) на дійсній півосі. У функції Ai(x) на комплексній площині немає інших нулів, а а функція Bi(x) має нескінченне число нулів в секторі {z∈C : (1/3)π < |arg z| < (1/2)π}.

Для додатних аргументів, функції Ейрі зв'язані з модифікованими функціями Бесселя:

${\displaystyle {\begin{aligned}\mathrm {Ai} (x)&{}={\frac {1}{\pi }}{\sqrt {{\frac {1}{3}}x}}\,K_{1/3}\left({\frac {2}{3}}x^{3/2}\right),\\\mathrm {Bi} (x)&{}={\sqrt {{\frac {1}{3}}x}}\left(I_{1/3}\left({\frac {2}{3}}x^{3/2}\right)+I_{-1/3}\left({\frac {2}{3}}x^{3/2}\right)\right).\end{aligned}}}$

де I_±1/3 и K_1/3 — розв'язок рівняння ${\displaystyle x^{2}y''+xy'-(x^{2}+1/9)y=0\,}$.

Для від'ємних аргументів функції Ейрі зв'язані з функціями Бесселя:

${\displaystyle {\begin{aligned}\mathrm {Ai} (-x)&{}={\frac {1}{3}}{\sqrt {x}}\left(J_{1/3}\left({\frac {2}{3}}x^{3/2}\right)+J_{-1/3}\left({\frac {2}{3}}x^{3/2}\right)\right),\\\mathrm {Bi} (-x)&{}={\sqrt {{\frac {1}{3}}x}}\left(J_{-1/3}\left({\frac {2}{3}}x^{3/2}\right)-J_{1/3}\left({\frac {2}{3}}x^{3/2}\right)\right).\end{aligned}}}$

де J_±1/3 — розв'язок рівняння ${\displaystyle x^{2}y''+xy'+(x^{2}-1/9)y=0\,}$.

Функції Скорера є розв'язками рівняння ${\displaystyle y''-xy=1/\pi \,}$. Вони також можуть бути виражені через функції Ейрі

${\displaystyle {\begin{aligned}\mathrm {Gi} (x)&{}=\mathrm {Bi} (x)\int _{x}^{\infty }\mathrm {Ai} (t)\,dt+\mathrm {Ai} (x)\int _{0}^{x}\mathrm {Bi} (t)\,dt,\\\mathrm {Hi} (x)&{}=\mathrm {Bi} (x)\int _{-\infty }^{x}\mathrm {Ai} (t)\,dt-\mathrm {Ai} (x)\int _{-\infty }^{x}\mathrm {Bi} (t)\,dt.\end{aligned}}}$

Функція Ейрі названа на честь британського астронома Джорджа Бідделя Ейрі, котрий зіткнувся з нею при оптичних дослідженнях (1838 р.). Позначення Ai(x) запровадив Гарольд Джеффрі.

• Розділ AI: Функції Ейрі і споріднені функції в Цифровій бібліотеці математичних функцій.

• Ландау Л. Д., Лившиц Е. М.: Квантовая механика, 1989 Розділ: Математические дополнения
• Milton Abramowitz and Irene A. Stegun (1954). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, ( § 10.4).
• Airy (1838). On the intensity of light in the neighbourhood of a caustic. Transactions of the Cambridge Philosophical Society, 6, 379—402.
• Olver (1974). Asymptotics and Special Functions, Chapter 11. Academic Press, New York.