Гамма-функція
Гамма-функція (позначається великою літерою грецького алфавіту — Гамма, Γ) —є одним із способів розширення функції факторіала, до дійсних і комплексних чисел, із зсувом її аргумента менше на 1. Даніель Бернуллі вивів цю функцію для n, що є додатнім цілим числом,
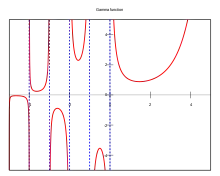
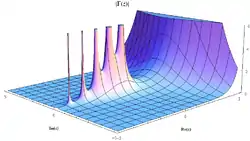
Хоча існують і інші подібні розширення, це конкретне визначення є найбільш популярним і вживаним. Гамма-функція визначена для всіх комплексних чисел, окрім не додатних цілих. Для комплексних чисел із додатною дійсною частиною, гамма-функція визначається через збіжний невласний інтеграл:
Цю інтегральну функцію за допомогою аналітичного продовження можна розширити для всіх комплексних чисел, крім недодатних цілих (де функція має прості полюси), в результаті чого отримують мероморфну функцію яку називають гамма-функцією. Вона не має нулів, тож взаємна гамма функція 1/Γ(z) є голоморфною функцією. Гамма-функція відповідає перетворенню Мелліна для від'ємної показникової функції:
Гамма-функція є складовою різних функцій розподілу імовірностей, тож вона використовуються в таких областях як теорія імовірностей і статистика, а також у комбінаториці.
Мотивування
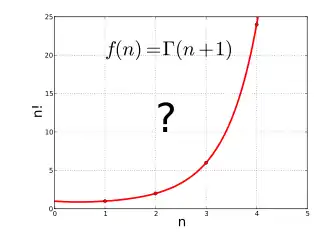
Гамма функцію можна розглядати як рішення наступної задачі інтерполяції:
- "Необхідно знайти гладку функцію яка сполучає точки (x, y) задані відношенням y = (x − 1)! при додатних цілих значеннях змінної x."
Графік перших декількох точок факторіалів дозволяє припустити, що така крива можлива, але було б бажано знайти формулу, яка точно описує цю криву, в якій кількість операцій не залежить від розміру x. Просту формулу для факторіалу, x! = 1 × 2 × … × x, не можна застосувати напряму для не цілих значень x оскільки вона є дійсною лише коли x є натуральним числом (тобто, додатним цілим). Просто кажучи, не існує простого рішення для факторіалів; ніякі нескінченні комбінації сумування, добутку, піднесення у степінь, показникових функцій, або логарифмів, які б були здатні виразити функцію x!; але можна знайти загальну формулу для факторіалів за допомогою таких засобів як інтеграли і границі із диференціального та інтегрального числення. Хорошим рішенням цієї задачі є гамма функція.[1]
Існує багато способів для поширення факторіалу до не цілих значень: через множину окремих точок можна провести нескінченну кількість різних кривих. Гамма-функція є одним із самих корисним вирішенням цієї задачі на практиці, оскільки вона є аналітичною функцією (крім області значень не додатних цілих).[1] Ще однією важливою особливістю цієї функції, це те що вона задовольняє рекурентному співвідношенню, що визначає аналогічну властивість функції факторіалу,
для x, що дорівнює будь-якому додатному дійсному числу. Це дозволяє множити її із будь-якою періодичною аналітичною функцією, яка матиме значення одиниці для додатних цілих, наприклад така функція як ek sin mπx.
Визначення
Основне визначення
Нотацію Γ(z) ввів Адрієн-Марі Лежандр.[1] Якщо дійсна частина комплексного числа z є додатною (Re(z) > 0), тоді інтеграл
є абсолютно збіжним, і відомий як інтеграл Ейлера другого роду (інтеграл Ейлера першого роду визначає бета-функцію).[1] Застосувавши інтегрування частинами, можна побачити, що:
Визначивши, що при тому як
Можемо розрахувати
Маємо що і
для всіх додатних цілих чисел n. Це є прикладом доведення методом математичної індукції.
Альтернативні визначення
Функція є неперервним продовженням факторіалу визначеного лише для значень на усю площину комплексної змінної Функція Ейлера може бути визначена однією з нижченаведених формул:
Вона задовільняє наступним співвідношенням:
Оскільки то позначається як Згідно до визначення факторіалу,
Біноміальний коефіцієнт виражається через гама-функцію наступним чином:
Можна також представити інтеграл через гама-функцію
який має назву Бета-функції. Таким чином,
[2]
Ейлерове визначення як нескінченного добутку
При пошуку наближення для z! для комплексного числа z, виявляється, що простіше спочатку порахувати n! для деякого великого цілого числа n, а потім використати це для апроксимації значення для (n+z)!, після чого використати рекурентне рівняння m! = m (m−1)! у зворотньому порядку n разів, для того, щоб зрештою апроксимувати z!. Крім того, ця апроксимація стає точною для границі із тим як n прямує до нескінченності.
Зокрема, для деякого цілого числа m, буде так, що
і ми хочемо, щоб та сама формула виконувалася, якщо довільне ціле m буде замінено на довільне комплексне число z
Помноживши обидві частини на z! отримаємо
Ця формула із нескінченним добутком є збіжною для всіх комплексних чисел z крім від'ємних цілих, оскільки при спробі використати рекурентне відношення m! = m (m − 1)! в зворотньому порядку до значення m = 0 призведе до ділення на нуль.
Аналогічно і гамма-функція, визначена відповідно до Ейлера як нескінченний добуток буде справедливою для всіх комплексних чисел за виключенням недодатних цілих:
При такій конструкції, гамма-функція є унікальною функцією, яка одночасно задовольняє рівнянням , для всіх комплексних чисел крім не додатних цілих, і для всіх комплексних чисел .[1]
Рівняння можна використати для однозначного розширення інтегральної формули для Γ(z) до мероморфної функції, визначеної для всіх комплексних чисел z, крім цілих, що менші або рівні нулю.[1] Саме ця розширена версія як правило називається гамма-функцією.[1]
Визначення Вейєрштрасса
Визначення гамма-функції, яке дав Вейєрштрасс також є дійсним для всіх комплексних чисел z, крім недодатних цілих:
Множина визначення
Інтеграл, яким визначається гама-функція є невласним, і збігається при . Однак, використовуючи рекурентне співвідношення
її можна продовжити на всю комплексну площину за винятком точок , де .
Гамма-функція є неперервною функцією з простору неперервних функціоналів Чебишова. Вона є стійкою за Адамаром, виражається за третім законом Лопіталя.
Часткові значення
Особливо важливі часткові значення гама-функції в певних точках
- — за означенням.
- — див. також факторіал.
Властивості
Загальні
Важливим функціональним рівнянням для гамма-функції є Єйлерова формула відображення
з якої випливає:
і Формула подвоєння Лагранжа
| Доведення Єйлерової формули відображення |
|---|
|
Оскільки гамма-функцію можна представити як Проінтегрувавши по частинам разів, отримаємо що дорівнює Це можна переписати наступним чином Потім, використавши функціональне рівняння для гамма-функції, отримаємо Використавши розкладання у ряд Фур'є, функцію можна представити наступним чином де і . Використавши тригонометричні тотожності, цей вираз можна спростити наступним чином: Якщо прийняти, що і розділити рівняння на отримаємо Тепер виконаємо заміну , щоб отримати Проінтегрувавши обидві сторони по інтервалу від до і звівши до степеня, отримаємо Тоді Звідси випливає формула відображення Ейлера: |
| Доведення формули множення Лагранжа |
|---|
|
Бета-функцію можна представити наступним чином Якщо задати отримаємо Виконавши заміну отримаємо Функція є парною, оскільки Тепер припустимо Тоді Звідси випливає Оскільки звідси отримаємо формулу подвоєння Лагранжа: |
Формула подвоєння є особливим випадком теореми про множення Лагранжа(див. [3], Eq. 5.5.6)
Простою, але корисною властивістю, яка випливає із визначення границі, це:
Зокрема, при z = a + bi, цей добуток дорівнює
Одним із самих відомих значень гамма-функції для нецілого аргумента є:
яке отримують, якщо задати z = 12 у формулах відображення або подвоєння, використавши рівняння для бета функції із x = y = 12, або виконавши заміну u = √x у визначенні інтегралу гамма-функції, із чого в результаті отримають Гаусів інтеграл. У загальному випадку, для невід'ємних цілих чисел n маємо:
де n!! позначає подвійний факторіал від n. Коли n = 0, n!! = 1.
Може здаватися, що поглянувши на формулу результат Γ(12) = √π можна узагальнити для інших окремих значень Γ(r) де r є раціональним числом. Однак, ці числа не можна виразити через самих себе в рамках елементарних функцій. Було доведено, що Γ(n + r) є трансцендентним числом і алгебраїчно незалежним від π для будь-якого цілого n і будь-якого дробу із r = 16, 14, 13, 23, 34, 56.[4] У загальному випадку, для розрахунку значень гамма-функції необхідно застосовувати числову апроксимацію.
Іншою корисною границею для асимптотичного наближення є:
Похідні гамма-функції можна описати за допомогою полігамма-функції. Наприклад:
Для додатного цілого числа m похідну гамма-функції можна розрахувати наступним чином (тут γ це Стала Ейлера—Маскероні):
Для Re(x) > 0 n-а похідна гамма-функції дорівнює:
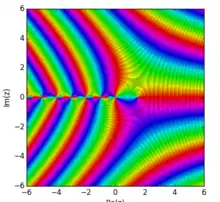
(Це можна отримати за допомогою диференціювання інтегралу для гамма-функції по змінній x, і використавши інтегральне правило Лейбніца.)
Використавши рівняння
де ζ(z) - дзета-функція Рімана, із розбиттям
зокрема маємо
Нерівності
Якщо обмежитися додатними цілими числами, гамма-функція є суворо логарифмічно опуклою функцією. Цю властивість можна визначити за допомогою трьох наведених еквівалентних нерівностей:
- Для будь-яких двох додатних дійсних чисел x1 і x2, і для будь-якого t ∈ [0, 1],
Крім того, ця нерівність буде точною для t ∈ (0, 1).
- Для будь-яких двох додатних дійсних чисел x і y при y > x,
- Для будь-якого додатного дійсного числа x,
Останні два твердження, випливають із визначення, так само як і твердження, що , де це полігамма-функція порядку 1. Аби довести логарифмічну опуклість гамма-функції достатньо спостерігати, що має ряд представлень для яких, при додатному дійсному x вона складається лише із додатних термів.
Логарифмічна опуклість і нерівність Єнсена разом означають, що для будь-яких додатних дійсних чисел and ,
Існують також обмеження відношення гамма-функцій. Найвідомішим є Нерівність Гаутсі, яка стверджує, що для будь-якого додатного цілого числа x і будь-якогоs ∈ (0, 1),
Формула Стірлінґа
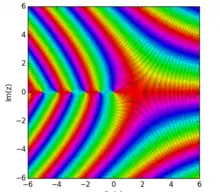
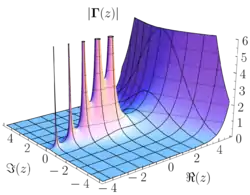
Поведінка функції для зростаючих цілих значень змінної є простою: вона зростає досить швидко — швидше за показникову функцію. Асимптотично при , величина гамма-функції задається за допомогою формули Стірлінґа
де символ задає відношення з яким обидві сторони збігаються до 1[1] або асимптотично сходяться.
Наближення
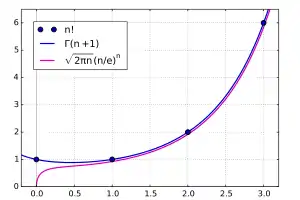
Комплексні значення гамма-функції можна обчислити чисельним способом із довільною точністю використовуючи формулу Стірлінга або наближення Ланцоса.
Гамма-функцію можна обрахувати із сталою точністю для Re(z) ∈ [1,2] застосувавши до інтеграла Ейлера метод інтегрування частинами. Для будь-якого додатнього числа x гамма-функцію можна записати як
Коли Re(z) ∈ [1,2] і x ≥ 1, абсолютне значення останнього інтегралу є меншим за (x + 1)e−x. Якщо вибрати достатньо велике x, цей вираз може бути меншим за 2−N для будь-якого бажаного значення N. Тож, за допомогою вищевказаного ряду гамма-функцію можна обрахувати до N бітів точності.
Швидкий алгоритм для розрахунку Ейлерової гамма-функції для будь-якого алгебраїчного аргументу (в тому числі раціонального) Е.А. Карацуба,[5][6][7]
Для аргументів, які є цілими кратними для 124, гамма-функцію також можна швидко розрахувати використавши ітерації для середнього арифметико-геометричного.
Застосування для формули Стірлінга
Наступний розклад в ряд гамма-функції для великих цілих дає асимптотичний вираз для формули Стірлінга, що використовується для обчислення факторіалу цілого числа.
Історія
Позначення гама-функції ввів у обіг Лежандр.
Див. також
Джерела
- Підкуйко, Сергій (2004). Математичний аналіз — Т.1. Множини. Дійсні числа. Границя послідовності. Границя функції. Неперервність функції. Диференціальне числення функцій однієї змінної. Львів: Галицька видавнича спілка. с. 530. ISBN 966-7893-26-Х Перевірте значення
|isbn=(довідка).
Примітки
- Davis, P. J. (1959). Leonhard Euler's Integral: A Historical Profile of the Gamma Function. American Mathematical Monthly 66 (10): 849–869. doi:10.2307/2309786. Процитовано 3 грудня 2016.
- А.М.Нахушев - Уравнения математической биологии.
- Шаблон:Dlmf
- Waldschmidt, M. (2006). Transcendence of Periods: The State of the Art. Pure Appl. Math. Quart. 2 (2): 435–463. doi:10.4310/pamq.2006.v2.n2.a3.

- E.A. Karatsuba, Fast evaluation of transcendental functions. Probl. Inf. Transm. Vol.27, No.4, pp. 339–360 (1991).
- E.A. Karatsuba, On a new method for fast evaluation of transcendental functions. Russ. Math. Surv. Vol.46, No.2, pp. 246–247 (1991).
- E.A. Karatsuba "Fast Algorithms and the FEE Method".
