Щасливе число (lucky number)
Щасливе число (англ. lucky number) в теорії чисел — натуральне число з множини, що генерується «решетом», аналогічним решету Ератосфена, яке генерує прості числа.
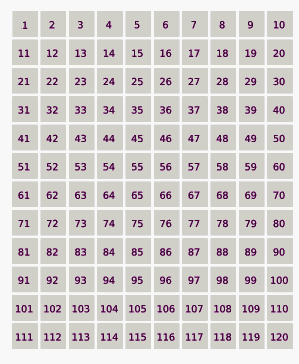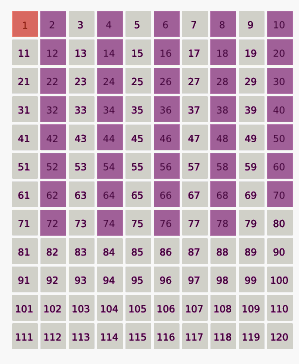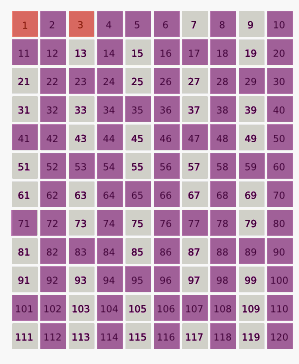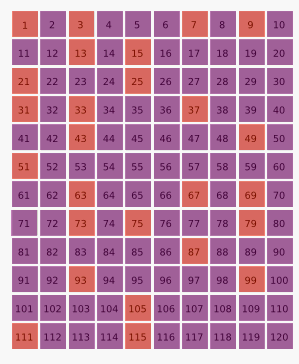
Процес «відсіювання» розпочинається з повного списку натуральних чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26...
Кожне друге число (тобто всі парні числа) вилучається, залишаються лише непарні числа:
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25...
Другий член новоутвореної послідовності — число 3. Тому кожне третє число з тих, що залишилися в списку, вилучається:
1, 3, 7, 9, 13, 15, 19, 21, 25...
Далі третім числом залишається — 7, отже кожен сьомий елемент нової послідовності вилучається:
1, 3, 7, 9, 13, 15, 21, 25...
Цей процес постійно повторюється; числа, що залишилися, і є щасливими числами:
- 1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, 87, 93, 99, 105, 111, 115, 127, 129, 133, 135, 141, 151, 159, 163, 169, 171, 189, 193, 195, 201, 205, 211, 219, 223, 231, 235, 237, 241, 259, 261, 267, 273, 283, 285, 289, 297, 303, 307, 319, 321, 327, 331, 339, 349, 357, 361, 367, 385, 391, 393, 399, 409, 415, 421, 427, 429, 433, 451, 463, 475, 477, 483, 487, 489, 495, 511, 517, 519, 529, 535, 537, 541, 553, 559, 577, 579, 583, 591, 601, 613, 615, 619, 621, 631, 639, 643, 645, 651, 655, 673, 679, 685, 693, 699, 717, 723, 727, 729, 735, 739, 741, 745, 769, 777, … (послідовність A000959 з Онлайн енциклопедії послідовностей цілих чисел, OEIS).
Історія
У 1955 році термін запропоновано в роботі Гардінера, Лазаруса, Метрополіса і Уляма. Також вони запропонували назвати це решето решетом Йосипа Флавія[1] через його схожість із задачею Йосипа Флавія.
Властивості
Щасливі числа за багатьма властивостями близькі до простих чисел[2]. Наприклад, їх асимптотична щільність дорівнює тобто збігається з асимптотичною щільністю простих чисел; щасливі числа-близнюки і прості числа-близнюки також з'являються з близькою частотою. Пари щасливих чисел, що відрізняються на 4, 6, 8 і т. д., з'являються з частотою, близькою до частоти відповідних пар простих чисел. На щасливі числа можна поширити версію проблеми Гольдбаха[2]. Існує безліч щасливих чисел. Через ці очевидні зв'язки із простими числами деякі математики припустили, що ці властивості можна знайти у ширшому класі множин цих чисел, згенерованих решетом невідомого виду, хоча теоретичні основи для цієї гіпотези надто малі.
Щасливі прості числа
Щасливе просте число — це щасливе число, яке є простим. Невідомо, чи є нескінченною множина щасливих простих чисел. Першими числами цієї послідовності є числа:
- 3, 7, 13, 31, 37, 43, 67, 73, 79, 127, 151, 163, 193, … (послідовність A031157 з Онлайн енциклопедії послідовностей цілих чисел, OEIS).
Примітки
- V. Gardiner, R. Lazarus, N. Metropolis and S. Ulam, «On certain sequences of integers defined by sieves», Mathematics Magazine 29:3 (1955), pp. 117—122.
- Нерешённые математические задачи, 1964, с. 137-138.
Література
Посилання
- Peterson, Ivars. MathTrek: Martin Gardner's Lucky Number (англ.)
- Weisstein, Eric W. Щасливі числа(англ.) на сайті Wolfram MathWorld.
- Lucky Numbers by Enrique Zeleny, The Wolfram Demonstrations Project (англ.)