Ортогональна опукла оболонка

В геометрії, множина K ⊂ Rn буде ортогонально опуклою, якщо для будь-якої прямої L, паралельної одному зі стандартних базисних векторів Rn, перетин K з L буде або порожнім або точкою або відрізком. Термін «ортогональний» відноситься до відповідного декартового базису і координат в евклідовому просторі, де різні базисні вектори перпендикулярні, а також до відповідних прямих. На відміну від звичайних опуклих множин, ортогонально опукла оболонка не обов'язково буде зв'язною множиною.

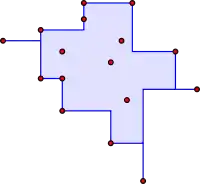
Ортогональна опукла оболонка множини точок

Ортогональна опукла оболонка множини S ⊂ Rn є перетином всіх зв'язних ортогонально опуклих множин, що містять S.

Ці визначення зроблені за аналогією з класичною теорією опуклості, в якій множина K є опуклою, якщо для будь-якої прямої L, перетин К з L буде порожньою множиною, точкою, або сегментом (інтервалом). Ортогональна опуклість обмежує множину прямих, для яких ця властивість виконується. Таким чином, кожна опукла множина буде ортогонально опуклою але не навпаки. З тієї ж причини, ортогональна опукла оболонка сама є підмножиною опуклої оболонки того ж набору точок. Точка р належить ортогональній опуклій оболонці S тоді і тільки тоді, коли кожен із закритих, вирівняних по осях ортів, що містить р як вершину, має непорожній перетин з S.

Ортогональна опукла оболонка також відома як прямолінійна опукла оболонка, або, двовимірна х-у опукла оболонка.

Приклад

На малюнку показано набір з 16 точок на площині та їх ортогональна опукла оболонка. Як можна бачити на малюнку, ортогональна опукла оболонка являє собою багатокутник, який містить вироджені ребра, що з'єднують крайні вершини в кожному координатному напрямку. Для дискретної множини точок, такій як ця, усі ортогональні опуклі краї оболонки горизонтальні або вертикальні. У наведеному прикладі ортогональна опукла оболонка зв'язна.

Алгоритми

Наступні автори досліджували алгоритми побудови ортогональних опуклих оболонок: Montuno & Fournier (1982[1]); Nicholl et al. (1983[2]); Ottman, Soisalon-Soisinen & Wood (1984[3]); Karlsson & Overmars (1988[4]). У підсумку можна стверджувати, що ортогональна опукла оболонка K точок на площині може бути побудовано за час O(k log k), або, можливо, і швидше, якщо використовувати цілочисельні пошукові структури даних для точок з цілими координатами.

Пов'язані поняття

Природно узагальнити ортогональну опуклість, як обмежено орієнтовану опуклість, в якій множина K є опуклою, якщо кожна пряма, яка паралельна одному з кінцевого набору напрямків, перетинає K по зв'язній підмножині; див., наприклад Rawlins(1987[5] ), Rawlins та Wood (1987[6], 1988[7]), або Fink та Wood (1996[8], 1998[9]).

Крім того, метрична обгортка метричного простору тісно пов'язана з ортогональною опуклою оболонкою. Якщо скінченна множина точок на площині має зв'язну ортогонально опуклу оболонку, тоді оболонка буде метричною обгорткою для манхеттенської метрики на множині точок. Проте, ортогональна оболонка і метрична обгортка відрізняються у випадку множин точок з незв'язною ортогональною оболонкою, або в багатовимірних L р просторах.

O'Rourke (1993[10]) описує дещо інші результати по ортогональній опуклості і ортогональній видимості.

Посилання
  1. Montuno, D. Y.; Fournier, A. (1982). Finding the x-y convex hull of a set of x-y polygons. Technical Report 148. University of Toronto..
  2. Nicholl, T. M.; Lee, D. T.; Liao, Y. Z.; Wong, C. K. (1983). On the X-Y convex hull of a set of X-Y polygons. BIT 23 (4): 456–471. doi:10.1007/BF01933620..
  3. Ottman, T.; Soisalon-Soisinen, E.; Wood, Derick (1984). On the definition and computation of rectilinear convex hulls. Information Sciences 33 (3): 157–171. doi:10.1016/0020-0255(84)90025-2..
  4. Karlsson, Rolf G.; Overmars, Mark H. (1988). Scanline algorithms on a grid. BIT 28 (2): 227–241. doi:10.1007/BF01934088..
  5. Rawlins, G. J. E. (1987). Explorations in Restricted-Orientation Geometry. Ph.D. thesis and Tech. Rep. CS-87-57. University of Waterloo..
  6. Rawlins, G. J. E.; Wood, Derick (1987). Optimal computation of finitely oriented convex hulls. Information and Computation 72 (2): 150–166. doi:10.1016/0890-5401(87)90045-9..
  7. Rawlins, G. J. E.; Wood, Derick (1988). Ortho-convexity and its generalizations. У Toussaint, Godfried T.. Computational Morphology. Elsevier. с. 137–152.
  8. Fink, Eugene; Wood, Derick (1996). Fundamentals of restricted-orientation convexity. Information Sciences 92 (1–4): 175–196. doi:10.1016/0020-0255(96)00056-4..
  9. Fink, Eugene; Wood, Derick (1998). Generalized halfspaces in restricted-orientation convexity. Journal of Geometry 62: 99–120. doi:10.1007/BF01237603..
  10. O'Rourke, Joseph (1993). Computational Geometry in C. Cambridge University Press. с. 107–109..
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.