Алгоритм Форчуна

Оскільки задача сортування дійсних чисел зводиться до задачі обчислення діаграми Вороного, то маємо, що довільний алгоритм для обчислення діаграми Вороного потребує ${\displaystyle \Omega (n\log n)}$ часу в найкращому випадку. Отже, алгоритм Форчуна — оптимальний.

Нехай ${\displaystyle P:=\{p_{1},p_{2},\dots ,p_{n}\}}$ буде множиною точок на площині. Позначимо діаграму Вороного для ${\displaystyle P}$ як ${\displaystyle {\mbox{Vor}}(P).}$ Як ${\displaystyle {\mbox{Vor}}(P)}$ також позначимо тільки ребра і вершини розбиття. Комірку ${\displaystyle {\mbox{Vor}}(P),}$ яка відповідає точці ${\displaystyle p_{i}}$ позначимо як ${\displaystyle {\mathcal {V}}(p_{i}).}$

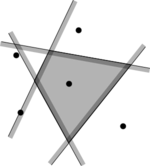
Для двох точок ${\displaystyle p}$ та ${\displaystyle q}$ на площині ми визначаємо бісектор для ${\displaystyle p}$ та ${\displaystyle q}$ як перпендикулярний бісектор відрізку ${\displaystyle {\overline {pq}}}$. Цей бісектор розбиває площину на дві півплощини. Позначимо півплощину, що містить ${\displaystyle p}$ як ${\displaystyle h(p,q)}$, а іншу півплощину, що містить ${\displaystyle q}$, як ${\displaystyle h(q,p).}$ Зауважимо, що ${\displaystyle r\in h(p,q)}$ тоді і тільки тоді, якщо відстані ${\displaystyle dist(r,p)<dist(r,q).}$ З цього випливає таке спостереження:

Отже, ${\displaystyle {\mathcal {V}}(p_{i})}$ є перетином ${\displaystyle n-1}$ півплощини і, звідси, можливо необмеженим відкритим опуклим полігональним регіоном з не більше ніж ${\displaystyle n-1}$ вершиною і не більше ніж ${\displaystyle n-1}$ ребром.

Теорема колінеарних точок: Нехай ${\displaystyle P}$ буде множиною з ${\displaystyle n}$ точок на площині. Якщо всі точки лежать на одній прямій, то ${\displaystyle {\mbox{Vor}}(P)}$ складається з ${\displaystyle n-1}$ паралельної лінії. Інакше, ${\displaystyle {\mbox{Vor}}(P)}$ зв'язна і її ребра це будуть або відрізки, або промені.

Точка у середині кола із трьома точками на колі (червоне) є вершиною, із двома точками на ньому (фіолетове) лежить на ребрі діаграми Вороного

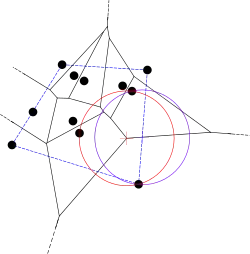
Теорема вершин і ребер: Для діаграми Вороного ${\displaystyle {\mbox{Vor}}(P)}$ правильно таке:

1. Точка ${\displaystyle q}$ є вершиною ${\displaystyle {\mbox{Vor(P)}}}$, якщо найбільше порожнє коло ${\displaystyle C_{p}(q)}$ має три або більше точок у себе на границі.
2. Бісектор між точками ${\displaystyle p_{i}}$ і ${\displaystyle p_{j}}$ визначає ребро ${\displaystyle {\mbox{Vor(P)}}}$ тоді і тільки тоді, якщо існує ${\displaystyle q,}$ що лежить не ньому для якої ${\displaystyle C_{p}(q)}$ має саме ці дві точки на своїй границі і жодного іншого.

Для обчислення діаграми Вороного в алгоритмі Форчуна використовується метод лінійної розгортки. Ми маємо ${\displaystyle P=\{p_{1},p_{2},\dots ,p_{n}\}.}$ Нашу лінію розгортки ми позначимо як ${\displaystyle \ell .}$ У перебігу алгоритму ми повинні рухати нашу пряму розгортки згори додолу і під час цього руху підтримувати перетин ${\displaystyle {\mbox{Vor(P)}}}$ із цією лінією. Але це не так просто, оскільки частина ${\displaystyle {\mbox{Vor(P)}}}$ залежить частково і від точок, що розташовані під ${\displaystyle \ell .}$

Берегова лінія для діаграми Вороного позначена червоним

Позначимо замкнену півплощину над ${\displaystyle \ell }$ як ${\displaystyle \ell ^{+}.}$ ${\displaystyle \forall q\in \ell ^{+}}$ відстань від ${\displaystyle q}$ до будь-якої точки під ${\displaystyle \ell }$ більша ніж відстань від ${\displaystyle q}$ до самої ${\displaystyle \ell .}$ Отже, найближча до ${\displaystyle q}$ точка не може бути нижчим від ${\displaystyle \ell }$ якщо ${\displaystyle q}$ щонайменше так близько до якогось місця ${\displaystyle p_{i}\in \ell ^{+}}$ як ${\displaystyle q}$ близько до ${\displaystyle \ell .}$ Геометричне місце точок, які ближче до деякої точки ${\displaystyle p_{i}\in \ell ^{+}}$ ніж до ${\displaystyle \ell }$ обмежене параболою, оскільки її ексцентриситет дорівнює 1. Ми будемо називати послідовність таких параболічних дуг береговою лінією.

Спостереження: берегова лінія є ${\displaystyle x-}$монотонною, тобто кожна вертикальна пряма перетинає її саме в одній точці.

Зауважимо, що точки зустрічі різних параболічних дуг лежать на ребрах діаграми Вороного. Ці точки точно відслідковують ${\displaystyle {\mbox{Vor(P)}}}$ поки лінія розгортки рухається додолу. Отже, замість підтримування перетину діаграми з ${\displaystyle \ell }$ ми будемо відслідковувати берегову лінію. Ми не будемо зберігати параболи явно і не будемо відслідковувати берегову лінію неперервно, натомість ми будемо відслідковувати появу і зникнення дуг на ній.

Подія кола створюється

Подія кола не створюється

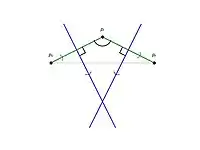
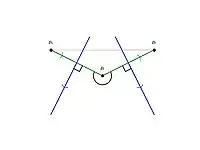
Параболічні дуги задаються так:

Тобто, найнижча точка параболи у ${\displaystyle (p_{i,x},(p_{i,y}+l_{y})/2),}$ а множник ${\displaystyle 1/[2(p_{i,y}-l_{y})]}$ переводить дугу з суто вертикальної прямої у момент появи точки на ${\displaystyle \ell }$ до все ширшої і ширшої параболи з тим як ${\displaystyle \ell }$ рухається додолу.

Назвемо подією місця, подію коли пряма розгортки зустрічає точку. У цей момент утворюється нова дуга.

Лема появи дуги: Єдиним способом появи нової дуги на береговій лінії є подія місця.

Назвемо подію коли берегова пряма досягає найнижчої точки кола на границі якого є не менше трьох точок, що визначають послідовні дуги на береговій лінії подією кола.

Лема зникнення дуги: Єдиним способом зникнення дуги з берегової лінії є подія кола.

Лема: Кожна вершина ${\displaystyle {\mbox{Vor}}(P)}$ виявлена за допомогою події кола.

Щоб виявити подію кола щодо певної дуги ${\displaystyle \alpha }$ місця ${\displaystyle p_{i}}$, треба перевірити, чи збігаються точки зустрічі цієї дуги з сусідніми дугами місць ${\displaystyle p_{s}}$ та ${\displaystyle p_{r},}$ тобто чи буде точка перетину прямих ${\displaystyle l_{1}}$ та ${\displaystyle l_{2},}$ на яких лежать ребра діаграми Вороного, лежати нижче берегової лінії. Оскільки лінії ${\displaystyle l_{1}}$ і ${\displaystyle l_{2}}$ перпендикулярні відповідно відрізкам ${\displaystyle p_{s}p_{i}}$ та ${\displaystyle p_{i}p_{r},}$ а їхні напрямки узгоджені (див рис.), то ця умова еквівалентна тому, що ${\displaystyle \angle p_{s}p_{i}p_{r}<\pi }$. Це, у свою чергу, свідчить про лівоорієнтованість трикутника ${\displaystyle p_{s}p_{i}p_{r}}$. З властивостей орієнтованої площі трикутника виплоиває, що точки зустрічі збігаються тоді і тільки тоді, коли

${\displaystyle {\begin{vmatrix}p_{i}.x-p_{s}.x&p_{r}.x-p_{s}.x\\p_{i}.y-p_{s}.y&p_{r}.y-p_{s}.y\\\end{vmatrix}}<0.}$

Ми хочемо обчислити діаграму Вороного, отже нам потрібні структури, які зберігають частину діаграми яку ми вже обчислили. Також нам потрібні дві стандартні для алгоритмів лінійної розгортки структури: черга подій і структура яка представляє статус лінії розгортки ${\displaystyle \ell .}$

• Ми зберігаємо діаграму Вороного під час побудови як подвійно зв'язаний список ребер. Однак, діаграма Вороного не є правильним розбиттям площини, тому що вона має нескінченні ребра, і подвійно зв'язаний список ребер не може представити таку структуру. Під час побудови це не проблема, оскільки представлення берегової лінії наведене далі уможливить ефективний доступ під час побудови до необхідних частин подвійно зв'язаного списку ребер. Для виправлення цього, ми додамо великий обмежувальний прямокутник навколо сцени. Кінцеве розбиття, яке ми обчислимо, складатиметься з обмежувального прямокутника і діаграми Вороного всередині.

• Берегова лінія представлена збалансованим деревом пошуку ${\displaystyle {\mathcal {T}};}$ це і статус-структура. Її листи відповідають дугам берегової лінії, які ${\displaystyle x-}$монотонні, впорядкованим чином: найлівіший лист представляє найлівішу дугу, і т. д. Кожен лист ${\displaystyle \mu }$ зберігає точку, що визначає дугу на береговій лінії. Внутрішні вузли ${\displaystyle {\mathcal {T}};}$ представляють точки зустрічі на береговій лінії. Точка зустрічі зберігається у вузлі як впорядкований кортеж точок ${\displaystyle p_{i},p_{j},}$ де ${\displaystyle p_{i}}$ визначає параболу ліворуч від точки зустрічі, а ${\displaystyle p_{j}}$ визначає параболу праворуч. Використовуючи це представлення, ми можемо знайти за ${\displaystyle O(n\log n)}$ дугу на береговій лінії, що лежить над новим місцем. У внутрішньому вузлі ми просто порівнюємо ${\displaystyle x-}$координати точок і точки зустрічі, яку можна обчислити з кортежу точок і позиції прямої розгортки у константний час.

У ${\displaystyle {\mathcal {T}}}$ ми також зберігаємо вказівники на інші дві структури даних використовувані впродовж розгортки. Кожен лист ${\displaystyle {\mathcal {T}},}$ представляє дугу ${\displaystyle \alpha ,}$ зберігає зберігає вказівник до вузла в черзі подій, який представляє подію кола в якій ${\displaystyle \alpha }$ зникне. Якщо такої події немає, то вказівник нульовий. Нарешті, кожен внутрішній вузол ${\displaystyle \nu }$ має вказівник на одне з півребер ребра, що відслідковується точкою зустрічі представленою ${\displaystyle \nu .}$

• Черга подій ${\displaystyle {\mathcal {Q}}}$ реалізована як черга з пріорітетом, де пріоритет це ${\displaystyle y-}$координата. Вона зберігає надхідні події, що вже відомі. Для події місця ми просто зберігаємо місце. Для події кола ми зберігаємо найнижчу точку кола із вказівником на лист ${\displaystyle {\mathcal {T}},}$ що представляє дугу, яка зникне у події.

Тут ми опишемо алгоритм лінійної розгортки детально. Зауважимо, що після обробки всіх подій, коли черга подій ${\displaystyle {\mathcal {Q}}}$ спорожніла, берегова лінія ще не зникла. Точки зустрічі, що досі присутні відповідають до ребер-променів діаграми Вороного. Оскільки подвійно зв'язаний список ребер не може представляти напів-нескінченні ребра, ми повинні додати обмежувальний прямокутник до якого можна буде прикріпити ці ребра.

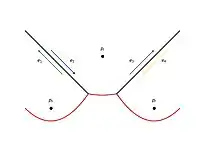До події кола 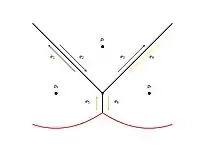Після події кола ОбробитиПодіюКола${\displaystyle (\gamma )}$ Видалити лист ${\displaystyle \gamma ,}$ який представляв дугу ${\displaystyle \alpha }$ місця ${\displaystyle p_{i},}$ що зникає з ${\displaystyle {\mathcal {T}}.}$ Оновити кортежі, що представляють точки зустрічей у внутрішніх вузлах, а саме, якщо зліва від ${\displaystyle \alpha }$ була дуга для ${\displaystyle p_{s},}$ а справа — дуга для ${\displaystyle p_{r},}$ то мають бути видалені вузли ${\displaystyle <p_{s},p_{i}>,<p_{i},p_{r}>}$ та створено вузол для точки зустрічі ${\displaystyle <p_{s},p_{r}>}$; зберегти півребра ${\displaystyle e_{1},e_{2},e_{3},e_{4},}$ що відповідали вузлам, які видаляються. Видалити з ${\displaystyle {\mathcal {Q}}}$ події кіл, на які посилаються сусідні до ${\displaystyle \gamma }$ листи, якщо ці вказівники були встановлені. (Подія кола, де ${\displaystyle \alpha }$ це середня дуга зараз обробляється і її вже видалено з ${\displaystyle {\mathcal {Q}}.}$) Додати центр кола, що спричинило подію як запис вершини у діаграму Вороного, що ми будуємо. Створити два записи для півребер, що відповідають новій точці зустрічі на береговій лінії (на рис. це близнюки ${\displaystyle e_{5},e_{6}}$). Встановити вказівники між півребрами, новою вершиною та гранями згідно зі структурою подвійно зв'язаного списку ребер. Перевірити нову трійку послідовних дуг, що має колишнього лівого сусіда дуги ${\displaystyle \alpha }$ як середню дугу на збіжність двох її точок зустрічей. Якщо так, вставити відповідні події кіл у ${\displaystyle {\mathcal {Q}}.}$ І встановити необхідні вказівники між новими подіями кіл у ${\displaystyle {\mathcal {Q}}}$ і листами ${\displaystyle {\mathcal {T}}.}$ Зробити те саме для трійки, де середньою дугою є колишній правий сусід ${\displaystyle \alpha .}$