Бісекція
В геометрії бісекція — це поділ чогось на дві рівні або конгруентні частини, як правило, прямою, яку потім називають бісектрисою. Найчастіше розглядаються такі типи бісектрис — бісектриса відрізка (пряма, яка проходить через середину даного відрізка) та бісектриса кута (пряма, яка проходить через вершину кута і ділить його на два рівні кути).

У тривимірному просторі бісекція зазвичай виконується площиною, яку також називають бісектрисою або бісектрисною площиною.
У тривимірному просторі бісекція зазвичай виконується площиною, яку також називають бісектрисою або бісектрисною площиною.
Бісектриса відрізка
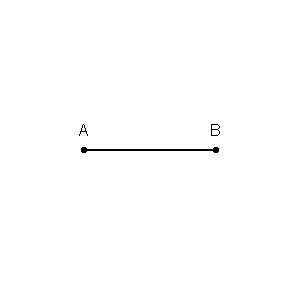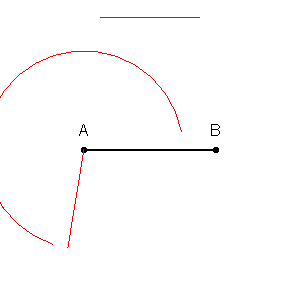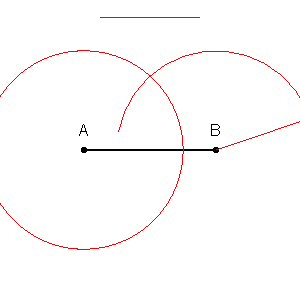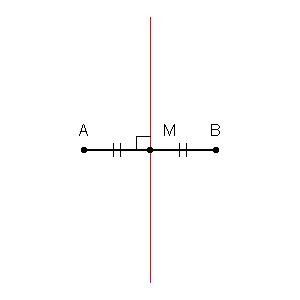
Бісектриса відрізка проходить через середину відрізка. Особливо важливою є перпендикулярна до відрізка бісектриса, яка, відповідно до назви, перетинає відрізок під прямим кутом. Перпендикулярна до відрізка бісектриса має властивість, що кожна його точка рівновіддалена від кінців відрізка.
У класичній геометрії виконання побудови бісекції за допомогою циркуля та лінійки, можливо завдяки тому, що можливо створювати кола рівних радіусів та з різними центрами. Наприклад, для поділу відрізка навпіл, будують кола однакового радіуса, які перетинаються та центри яких є кінцями відрізка. Пряма, визначена точками перетину двох таких кіл, є перпендикулярною бісектрисою відрізка, оскільки вона перетинає відрізок у його центрі. Ця побудова фактично використовується під час побудови прямої, перпендикулярної даній прямій у заданій точці: а саме, малюють довільне коло, центром якого є ця точка, це коло перетинає пряму ще в двох точках, а перпендикуляр, який потрібно побудувати, — той, що ділить навпіл відрізок, визначений цими двома точками.
Теорема Брахмагупти стверджує, що якщо вписаний чотирикутник — ортодіагональний (тобто має перпендикулярні діагоналі), то перпендикуляр до однієї з сторін, що проходить через точку перетину діагоналей, завжди ділить протилежну сторону навпіл.
В аналітичній формі бісектриса перпендикулярна до відрізка з кінцями і задається рівнянням
- , де , , і .
Бісектриса кута
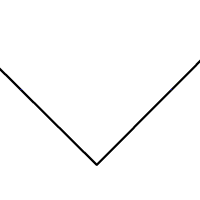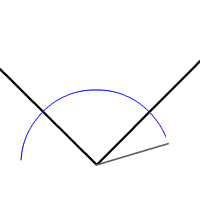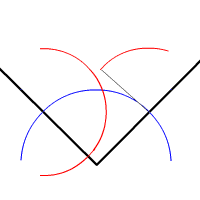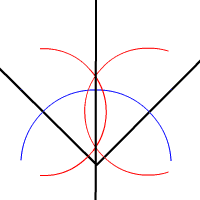
Бісектриса кута ділить кут на два кути з однаковими мірами. Кут має лише одну бісектрису. Кожна точка бісектриси кута рівновіддалена від сторін кута.
Внутрішня бісектриса кута — це пряма, промінь або відрізок, який ділить кут менше 180° на два рівні кути. Зовнішня бісектриса — це пряма, яка ділить додатковий кут (180° мінус початковий кут), утворений однією стороною, що утворює початковий кут, і продовженням другої сторони, на два рівні кути.[1]
Щоб здійснити бісекцію кута лінійкою та циркулем, зображають коло, центром якого є вершина кута. Коло перетинає кут у двох точках: по одній на кожній стороні кута. Використовуючи кожну з цих точок як центр, малюють два кола однакових радіусів. Перетин кіл (дві точки) визначає пряму, яка є бісектрисою кута.
Доведення цієї побудови досить інтуїтивно зрозуміле, якщо спиратись на симетричність задачі. Трисекцію кута (поділ його на три рівні частини) неможливо досягти лише циркулем та лінійкою (це вперше довів П'єр Ванцель).
Внутрішня та зовнішня бісектриси кута перпендикулярні. Якщо кут утворений двома прямими, заданими алгебраїчно рівняннями і то внутрішня та зовнішня бісектриси задаються двома рівняннями[2]
Трикутник
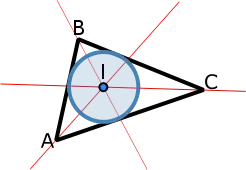
Перетини та колінеарність
Внутрішні бісектриси кута трикутника одночасно перетинаються в точці, яка називається стимулом (центром вписаного кола) трикутника, як видно на схемі праворуч.
Бісектриси двох зовнішніх кутів та бісектриса третьоговнутрішнього кута перетинаються в одній точці.[3]
Три точки перетину зовнішніх бісектрис кута з продовженнями протилежних їм сторін є колінеарними (лежать на одній прямій).[3]
Три точки перетину зовнішніх бісектрис кута з продовженнями протилежних їм сторін є колінеарними (лежать на одній прямій).[3]
Теорема про бісектрису кута
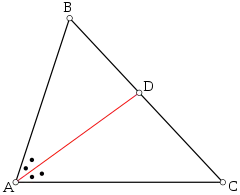
Теорема про бісектрису кута показує співвідношення довжин двох відрізків, на які сторона трикутника поділена прямою, що ділить навпіл протилежний кут. Теорема стверджує, що відношення цих відрізків дорівнює відношенню прилеглих до кута сторін.
Довжини
Якщо довжини сторін трикутника рівні , півпериметр а A — кут, протилежний стороні , тоді довжина внутрішньої бісектриси кута A дорівнює[3]
- або в тригонометричному вираженні,[4]
- Якщо внутрішня бісектриса кута A у трикутнику ABC має довжину і якщо ця бісектриса ділить сторону, протилежну А, на відрізки довжини m і n, то[3]
- ,
- де b і c — довжини сторін, протилежних вершинам B і C; а сторона, протилежна А, ділиться у пропорції b : c .
Якщо внутрішні бісектриси кутів A, B і C мають довжини і , тоді[5]
Цілочисельні трикутники
Існують цілочисельні трикутники з раціональною довжиною бісектриси кута.
Чотирикутник
Бісектриси внутрішніх кутів опуклого чотирикутника або утворюють вписаний чотирикутник (тобто чотири точки перетину сусідніх бісектрис кутів є конциклічними),[8] або паралельні. В останньому випадку чотирикутник є описаним чотирикутником.
Ромб
Кожна діагональ ромба ділить навпіл протилежні кути, тобто є їх бісектрисою.
Парабола
Дотична до параболи в заданій точці ділить навпіл кут між прямою, яка походить через задану точку та фокус параболи, і прямою, яка проходить через задану точку перпендикулярно до директриси параболи.
Бісектриси сторін многокутника
Медіани
Кожна з трьох медіан трикутника є відрізком прямої, що проходить через одну вершину та середину протилежної сторони, тому вона ділить цю сторону навпіл (в загальному випадку не перпендикулярно). Три медіани перетинають одна одну в центроїді трикутника, який називають також його центром маси; таким чином, будь-яка пряма, що проходить через центроїд трикутника та одна з його вершин, ділить навпіл протилежну сторону. Центроїд знаходиться вдвічі ближче до середини будь-якої сторони, ніж до протилежної вершини.
Бісектриси перпендикулярів
Внутрішньою перпендикулярною до сторони трикутника бісектрисою є відрізок, який повністю міститься у внутрішній області трикутника, і перпендикулярно ділить одну з сторін трикутника навпіл. Три такі бісектриси сторін трикутника перетинаються в центрі описаного кола (центр кола, що проходить через три вершини трикутника). Таким чином, будь-яка пряма, яка проходить через центр описаного кола трикутника і перпендикулярна стороні, ділить цю сторону навпіл.
У гострокутному трикутнику центр вписаного кола ділить внутрішні перпендикулярні бісектриси двох найкоротших сторін у рівних відношеннях. У тупокутному трикутнику перпендикулярні бісектриси двох коротших сторін (продовжені за межі трикутника до центру описаного кола) розділені третьою стороною трикутника у рівних відношеннях.[9]
Для будь-якого трикутника довжини внутрішніх перпендикулярних бісектрис задані формулами
і де сторони трикутника , а площа трикутника дорівнює [10]
Чотирикутник
Дві бімедіани опуклого чотирикутника — це відрізки, які з'єднують середини протилежних сторін, отже, кожна ділить дві сторони навпіл. Дві бімедіани і відрізок, що з'єднує середини діагоналей, перетинаються в точці, яка називається «центроїд вершини», і всі вони діляться навпіл на цій точці.[11]
Чотири відрізки опуклого чотирикутника, що є перпендикулярними до сторони чотирикутника і проходять через середину протилежної сторони, ділять сторону навпіл. Якщо чотирикутник вписаний у коло, ці відрізки лежать на конкурентних прямих і перетинаються у одній точці, яка називається «антицентром».
Теорема Брахмагупти стверджує, що якщо вписаний чотирикутник ортодіагональний (тобто має перпендикулярні діагоналі), то перпендикуляр до сторони від точки перетину діагоналей завжди ділить протилежну сторону навпіл.
Бісектриси площі та бісектриси периметра
Трикутник
Існує безліч прямих, які ділять площу трикутника навпіл. Три з них є медіанами трикутника (які з'єднують середини сторін з протилежними вершинами), і вони є перетинаються в центроїді трикутника; справді, це єдині бісектриси області, які проходить крізь центроїд. Три інші бісектриси площі паралельні сторонам трикутника; кожна з них перетинає дві інші сторони, ділячи їх у відношенні .[12]
Обгортка з нескінченності кількості бісектрис є дельтоїдою (в широкому сенсі, фігурою з трьома вершинами, з'єднаними кривими, які є увігнутими до зовнішньої частини).[12] Вершини дельтоїди розташовані на серединах медіан; всі точки всередині дельтоїди знаходяться на трьох різних бісектрисах площі, тоді як всі точки поза нею знаходяться лише на одній. Сторони дельтоїди — це дуги гіпербол, які є асимптотичними до продовжень сторін трикутника. Відношення площі обгортки бісектрис площі до площі трикутника є інваріантним для всіх трикутників і дорівнює тобто 0,019860 … або менше 2 %.
Колун[уточнити] трикутника — це відрізок, який ділить навпіл периметр трикутника і має один кінець в середині однієї з трьох сторін. Три колуни перетинаються в центрі Шпікера, який є центром вписаного кола в медіальний трикутник. Колун паралельний бісектрисі кута.
Розділювач трикутника — це відрізок прямої, що має один кінець в одній з трьох вершин трикутника і ділить периметр навпіл. Три розділювачі перетинаються в точці Наґеля трикутника.
Є прямі, які ділить площу трикутника та його периметр навпіл, і проходять через стимул трикутника (центр вписаного кола). Для будь-якого даного трикутника їх існує одна, дві або три. Пряма, що проходить через стимул, ділить навпіл площу (або периметр) тоді і лише тоді, коли вона також ділить навпіл периметр (або площу).[13]
Паралелограм
Будь-яка пряма через точку перетину діагоналей паралелограма ділить навпіл площу[14] та периметр паралелограма.
Коло і еліпс
Всі бісектриси площі та бісектриси периметра кола чи іншого еліпса проходять через центр кола (еліпса), а будь-які хорди через центр ділять площу та периметр навпіл. У випадку кола вони є діаметрами кола.
Бісектриси діагоналей
Паралелограм
Діагоналі паралелограма ділять навпіл одна одну.
Чотирикутник
Якщо відрізок, що з'єднує діагоналі чотирикутника, ділить навпіл обидві діагоналі, то цей відрізок прямої (пряма Ньютона) ділиться навпіл центроїдом вершини.
Бісектриси об'єму
Площина, яка ділить два протилежні ребра тетраедра в заданому співвідношенні, також ділить об'єм тетраедра в тому ж співвідношенні. Таким чином, будь-яка площина, що містить бімедіану (яка сполучає середини протилежних ребер) тетраедра, ділить навпіл об'єм тетраедра[15][16]
Література
- Weisstein, Eric W. «Exterior Angle Bisector.» From MathWorld - A Wolfram Web Resource.
- Spain, Barry. Analytical Conics, Dover Publications, 2007 (orig. 1957).
- Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).
- Oxman, Victor. «On the existence of triangles with given lengths of one side and two adjacent angle bisectors», Forum Geometricorum 4, 2004, 215—218. http://forumgeom.fau.edu/FG2004volume4/FG200425.pdf
- Simons, Stuart. Mathematical Gazette 93, March 2009, 115—116.
- Mironescu, P., and Panaitopol, L., «The existence of a triangle with prescribed angle bisector lengths», American Mathematical Monthly 101 (1994): 58–60.
- Oxman, Victor, «A purely geometric proof of the uniqueness of a triangle with prescribed angle bisectors», Forum Geometricorum 8 (2008): 197—200.
- Weisstein, Eric W. «Quadrilateral.» From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Quadrilateral.html
- Mitchell, Douglas W. (2013), «Perpendicular Bisectors of Triangle Sides», Forum Geometricorum 13, 53-59. http://forumgeom.fau.edu/FG2013volume13/FG201307.pdf
- Mitchell, Douglas W. (2013), "Perpendicular Bisectors of Triangle Sides", Forum Geometricorum 13, 53-59. http://forumgeom.fau.edu/FG2013volume13/FG201307.pdf
- Altshiller-Court, Nathan, College Geometry, Dover Publ., 2007.
- Dunn, J. A., and Pretty, J. E., "Halving a triangle, " Mathematical Gazette 56, May 1972, 105—108.
- Kodokostas, Dimitrios, "Triangle Equalizers, " Mathematics Magazine 83, April 2010, pp. 141—146.
- Dunn, J. A., and J. E. Pretty, «Halving a triangle», Mathematical Gazette 56, May 1972, p. 105.
- Weisstein, Eric W. «Tetrahedron.» From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Tetrahedron.html
- Altshiller-Court, N. «The tetrahedron.» Ch. 4 in Modern Pure Solid Geometry: Chelsea, 1979.
Посилання
- Бісектриса кута
- Визначення бісектриси кута. Відкритий довідник з математики
- Визначення бісектриси. Відкритий довідник з математики
- Бісектриса перпендикулярної прямої.
- Анімовані вказівки щодо поділу кута та поділу прямої за допомогою циркуля та лінійки
- Weisstein, Eric W. Line Bisector(англ.) на сайті Wolfram MathWorld.