Аперіодична мозаїка

Аперіодична мозаїка — це неперіодичне замощення з додатковою властивістю, що замощення не містить нескінченно великих періодичних шматків. Множина типів плиток (або протоплиток) є набором неперіодичних протоплиток, якщо копії цих плиток можуть утворювати тільки аперіодичні мозаїки. Мозаїки Пенроуза[1][2] є найвідомішими прикладами аперіодичних мозаїк.

Мозаїка Пенроуза є прикладом аперіодичних мозаїк. У будь-якій мозаїці, яку можна отримати з плиток Пенроуза, відсутня трансляційна симетрія

Аперіодичні мозаїки слугують математичними моделями для квазікристалів, фізичних тіл, відкритих у 1982 році Даном Шехтманом[3], який отримав у 2011 році Нобелівську премію[4]. Однак специфічна локальна структура цих матеріалів залишається погано зрозумілою.

Деякі методи побудови аперіодичних мозаїк відомі.

Визначення та ілюстрація

Розглянемо періодичну мозаїку з одиничних квадратів (вона виглядає як нескінченна міліметрівка). Тепер розділимо один квадрат на два прямокутники. Мозаїка, отримана таким чином, не є періодичною — не існує зсуву, що залишає цю мозаїку незмінною. Ясно, що цей приклад значно менш цікавий, ніж мозаїка Пенроуза. Щоб виключити такі приклади, аперіодична мозаїка визначається як така, що не містить довільно великих періодичних частин.

Мозаїка називається аперіодичною, якщо її оболонка містить тільки аперіодичні мозаїки. Оболонка замощення містить всі перенесення T+x замощення T разом з усіма замощеннями, які можна наблизити перенесенням T. Формально, це замикання множини у локальній топології[5]. В локальної топології (відповідної метриці) дві плитки -близькими, якщо вони однакові в колі радіуса навколо початку координат (можливо, після зсуву однієї з плиток на відстань, меншу від ).

Щоб навести ще простіший приклад, розглянемо одновимірне замощення T прямої, яке виглядає як …aaaaaabaaaaa… де a представляє інтервал одиничної довжини, а b представляє інтервал довжини два. Тоді замощення T складається з нескінченного числа копій a і однієї копії b (скажімо, з центром у точці 0). Тепер всі перенесення T є мозаїками з одним b десь і a в інших місцях. Послідовність мозаїк, у яких b має центр у точках сходиться (в локальній топології) до періодичної мозаїки, що складається тільки з плиток a. Таким чином, T не є аперіодичною мозаїкою, оскільки її замикання містить періодичну мозаїку …aaaaaa….

Для багатьох «хороших» замощень (наприклад, підстановок плиток з кінцевим числом локальних візерунків) виконується твердження: якщо мозаїка не містить періоду і повторюється (тобто кожна плитка зустрічається з однаковою ймовірністю в міру замощення), то вона аперіодична[6][5].

Історія

Перший раз питання про неперіодичні мозаїки постало 1961 року, коли логік Хао Ван спробував з'ясувати, чи може задача про доміно бути розв'язною, тобто чи існує алгоритм визначення, що заданий кінцевий набір протоплиток замощує площину. Ван знайшов алгоритми перерахування наборів плиток, які не можуть бути вкладені на площину, і наборів плиток, які замощують площину періодично. Тим самим він показав, що такий алгоритм існує, якщо для будь-якого скінченного набору протоплиток, який дозволяє замостити площину, також існує періодичне замощення. В 1964 році Роберт Берґер знайшов аперіодичний набір, тим самим показавши, що завдання замощення, фактично, нерозв'язне[7]. Це була перша така множина, що використовується в його доведенні нерозв'язності, і містила 20 426 плиток Вана. Берґер пізніше скоротив число плиток до 104, а Ганс Лейхлі (Hans Läuchli) знайшов аперіодичний набір із 40 плиток Вана[8]. Навіть менший набір з шести аперіодичних плиток (на базі плиток Вана) виявив Рафаель Робінсон у 1971 році[9]. Роджер Пенроуз знайшов три інших набори в 1973 і 1974 роках, скоротивши число необхідних плиток до двох, а Роберт Амманн виявив кілька інших наборів у 1977 році[8]. У 2010 році Соколаре і Тейлор знайшли набір з двох плиток однакового виду (правильні шестикутники), при цьому одна плитка симетрична інший [10].

Аперіодичні мозаїки Пенроуза можна утворити не тільки аперіодичними наборами протоплиток, а також за допомогою підстановки і методу «виріж-і-спроєктуй». Після виявлення квазікристалів аперіодичні мозаїки починають інтенсивно вивчати фізики і математики. Метод «виріж-і-спроєктуй» Н. Г. де Брейна для мозаїк Пенроуза врешті перетворився на частину теорії множин Меєра[11][12]. Нині існує багато літератури про аперіодичні мозаїки[5].

Побудови

Відомо кілька способів побудови аперіодичних мозаїк. Кілька побудов ґрунтуються на нескінченних сімействах аперіодичних наборів плиток [13][14]. Ці знайдені побудови працюють у більшості випадків декількома шляхами, головним чином за допомогою деякого виду аперіодичної ієрархічної структури. Попри це, нерозв'язність задачі доміно забезпечує, що має бути нескінченно багато різних побудов і, фактично, існують аперіодичні набори плиток, для яких не можна довести їхню аперіодичність.

Аперіодичні ієрархічні замощення

Досі не існує формального визначення, що описує, коли мозаїка має ієрархічну структуру. Проте ясно, що підстановка плиток таку структуру має, так само, як і мозаїки Берґера, Кнута, Лейхлі і Робінсона. Як і у випадку терміна «аперіодична мозаїка», термін «аперіодична ієрархічна мозаїка» є зручним скороченням, яке означає щось на зразок «набір плиток, які допускають тільки аперіодичні мозаїки з ієрархічною структурою».

Кожен з цих наборів плиток змушує будь-яку мозаїку з цих плиток мати ієрархічну структуру. (В багатьох наступних прикладах цю структуру можна описати як систему підстановки плиток, як це описано нижче). Ніяка мозаїка з цих наборів плиток не може бути періодичною просто тому, що ніяке паралельне перенесення не може залишити всю ієрархічну структуру незмінною. Розглянемо плитки Робінсона 1971 року:

Плитки Робінсона

Будь-яке замощення цими плитками може тільки дати ієрархію квадратних ґраток — кожен помаранчевий квадрат в кутку більшого квадрата, і так до нескінченності. Будь-яке паралельне перенесення повинне мати меншим від розміру будь-якого квадрата, а тому не може залишити таку мозаїку інваріантною.

Порція замощення плитками Робінсона

Робінсон довів, що ці плитки повинні утворювати структуру індуктивно. Як наслідок, плитки повинні утворювати блоки, які разом представляють збільшені варіанти початкових плиток і так далі. Ця ідея знаходження набору плиток, які можуть складати лише ієрархічні структури, досі використовується для побудови більшості відомих аперіодичних наборів плиток.

Підстановки

Системи підстановки плиток дають багате джерело аперіодичних мозаїк. Кажуть, що набір плиток, який змушує до виникнення структури підстановки, є змушеною структурою підстановки. Наприклад, плитки «стілець», показані нижче, допускають підстановку і фрагмент підстановки плиток показано на малюнку. Ці підстановки плиток обов'язково не є періодичними, але плитка «стілець» не є аперіодичною — легко знайти періодичне замощення цими плитками.

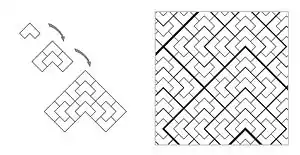
Система підстановки мозаїки для плитки «стілець».

Однак плитки, показані нижче, змушують виникнення структури підстановки плитки «стілець», а тому є аперіодичними[15].

Плитки «Трилобіт» і «Хрест» змушують структуру підстановки плитки «стілець» — вони можуть утворювати тільки мозаїки, в яких підстановка однозначно визначена і, тому, мозаїка є аперіодичною.

Плитки Пенроуза, а незабаром після цього деякі набори плиток Аммана[16] стали першими прикладами, заснованими на вимушених структурах підстановки плиток. Джошуа Соколар[17][18], Роджер Пенроуз [19], Людвіг Данцер[20] і Чайм Гудман-Штраус [15] знайшли кілька додаткових наборів. Шахар Мозес дав першу загальну побудову, показавши, що будь-який добуток одновимірних систем підстановки можна зробити вимушеним шляхом правил підстановки[14]. Чарльз Радін знайшов змушувальні правила для системи підстановки плиток для мозаїки Конвея «Вертушка» [21]. У 1998 Гудман-Штраус показав, що локальні правила з'єднання можна знайти для будь-якої структури підстановки плиток, що задовольняє деяким м'яким умовам[13].

Метод виріж-і-спроєктуй

Мозаїки без періодів можна отримати шляхом проєктування багатовимірних структур у простір з меншою розмірністю і за певних умов можуть існувати плитки, які перешкоджають цим структурам мати період, а тому мозаїки будуть аперіодичними. Плитки Пенроуза є першим і найвідомішим прикладом таких плиток, як було відмічено в роботі де Брейна[22]. Існує незакінчений (алгебричний) опис мозаїк «виріж і спроєктуй», які можна зробити вимушеними за допомогою правил з'єднання, хоча відомо багато необхідних і достатніх умов[23].

Деякі мозаїки, отримані методом «виріж і спроєктуй». Січні площини всі паралельні площині, яка визначає мозаїку Пенроуза (четверта мозаїка в третьому ряду). Ці мозаїки належать усі до різних локальних класів ізоморфізмів, тобто вони локально розпізнавані.

Інші техніки

Знайдено лише кілька інших видів побудов. Зокрема, Яркко Карі дав аперіодичний набір плиток Вана, заснований на добутках на 2 або на 2/3 дійсних чисел, закодованих рядами плиток (кодування пов'язане з послідовностями Штурма, отриманими як різниці послідовних елементів послідовності Бітті), з аперіодичністю, головним чином пов'язаною з фактом, що 2n/3m ніколи не дорівнює 1 для будь-якого з додатних цілих чисел n і m[24]. Цей метод пізніше Гудман-Штраус пристосував для отримання строго аперіодичного набору плиток на гіперболічній площині[25]. Шахар Мозес знайшов багато альтернативних побудов аперіодичних наборів плиток, деякі в більш екзотичному оточенні, наприклад у напівпростих групах Лі[26]. Блок і Вайнбергер використовували гомологічні методи для побудови аперіодичних наборів плиток для всіх неаменабельних многовидів[27]. Джошуа Соколар також дав інший спосіб змушення неперіодичності в термінах альтернувальних умов[28]. Це в загальному випадку веде до значно менших наборів плиток, ніж набір, отриманий з підстановок.

Фізика аперіодичних замощень

Аперіодичні мозаїки вважалися суто математичними об'єктами до 1984 року, коли фізик Дан Шехтман оголосив про відкриття різновиду алюмінієво-марганцевого сплаву, який давав чітку дифрактограму з недвозначною п'ятикратною симетрією[3]. Таким чином, ця речовина повинна бути кристалічною субстанцією з ікосоедральною симетрією. В 1975 році Роберт Амманн вже розширив побудова Пенроуза на тривимірний ікосоедральний еквівалент. У таких випадках термін «замощення» набуває сенсу «заповнення простору». Фотонні пристрої зараз будуються як аперіодичні послідовності різних шарів, які аперіодичні в одному напрямку і періодичні у двох інших. Виявилося, що структура квазікристалів Cd-Te складається з атомних шарів, у яких розташування атомів плоске аперіодичне. Іноді енергетичний мінімум або максимум ентропії проявляється саме на таких аперіодичних структурах. Пол Стейнгардт показав, що зчеплені десятикутники Гуммельта дозволяють застосувати принцип екстремуму і тим самим дають зв'язок між математичними неперіодичними мозаїками і структурою квазікристалів[29]. Спостерігалося явище, коли хвилі Фарадея утворювали великі фрагменти аперіодичних мозаїк[30]. Фізика цього відкриття воскресила інтерес до непропорційних структур і частот і з'явилося припущення про зв'язок аперіодичних мозаїк з явищем інтерференції[31].

Плутанина в термінології

Термін аперіодичний використовується в математичній літературі про мозаїки багатьма способами (а також в інших галузях математики, таких як динамічні системи та теорія графів, у зовсім іншому сенсі). Для мозаїк термін аперіодична іноді використовується як синонім неперіодичності. Неперіодична мозаїка — це мозаїка, в якій немає нетривіального паралельного перенесення. Іноді термін використовується, явно чи неявно, для опису мозаїк, утворених аперіодичним набором протоплиток. Часто термін туманно використовувався для опису структур фізичних аперіодичних речовин, а саме, квазікристалів, або чогось неперіодичного з деякого роду глобальним порядком.

Використання слів «мозаїка» або «замощення» також проблематичне, навіть за явного визначення термінів. Наприклад, немає єдиної мозаїки Пенроуза — ромби Пенроуза охоплюють нескінченне число мозаїк (які не розрізняються локально). У технічній літературі зазвичай намагаються уникати цих термінів, але терміни поширені як неформальні.

Див. також

Примітки
  1. Gardner, 1977, с. 111–119.
  2. Gardner, 1988.
  3. Schechtman, Blech, Gratias, Cahn, 1984, с. 1951–1953.
  4. Нобелевская премия по химии 2011.
  5. Baake, Grimm, 2013.
  6. Може здатися, що тут є тавтологія, проте відсутність періоду означає, що в цьому варіанті мозаїки періоду немає, а аперіодична мозаїка означає, що не можна за допомогою тих самих плиток створити періодичну мозаїку.
  7. Berger, 1966, с. 1–72.
  8. Grünbaum, Shephard, 1986, с. section 11.1.
  9. Robinson, 1971, с. 177–209.
  10. Socolar, Taylor, 2010.
  11. Lagarias, 1996, с. 356–376.
  12. Moody, 1997, с. 403–441.
  13. Goodman-Strauss, 1998, с. 181–223.
  14. Mozes, 1989, с. 39–186.
  15. Goodman-Strauss, 1999, с. 375–384.
  16. Grünbaum, Shephard, 1986.
  17. Senechal, 1995.
  18. Socolar, 1989, с. 10519–51.
  19. Penrose, 1997, с. 467–497.
  20. Nischke, Danzer, 1996, с. 221–236.
  21. Radin, 1994, с. 661–702.
  22. de Bruijn, 1981, с. 39–52, 53–66.
  23. Le, 1997, с. 331–366.
  24. Kari, 1996, с. 259–264.
  25. Goodman-Strauss, 2005, с. 119–132.
  26. Mozes, 1997, с. 603–611.
  27. Block, Weinberger, 1992, с. 907–918.
  28. Socolar, 1990, с. 599–619.
  29. Steinhardt.
  30. Edwards, Fauve, 1993.
  31. Levy, Mercier, 2006, с. 115.

Література
  • The Nobel Prize in Chemistry 2011. — Nobelprize.org. Процитовано 2011-10-06.
  • Martin Gardner. Mathematical Games // Scientific American. — 1977. — Т. 236 (January). — С. 111–119.
  • Martin Gardner.  — W H Freeman & Co, 1988. — ISBN 0-7167-1987-8.
  • Schechtman D., Blech I., Gratias D., Cahn J.W. Metallic Phase with long-range orientational order and no translational symmetry // Physical Review Letters. — 1984. — Т. 53, вип. 20 (19 листопада). — С. 1951–1953. — Bibcode:1984PhRvL..53.1951S. — DOI:10.1103/PhysRevLett.53.1951.
  • Baake M., Grimm U.  — Cambridge University Press, 2013.
  • Robert Berger. The undecidability of the domino problem // Memoirs of the American Mathematical Society. — 1966. — Т. 66 (19 листопада). — С. 1–72.
  • Raphael M. Robinson. Undecidability and Nonperiodicity for Tilings of the Plane // Inventiones Mathematicae. — 1971. — Т. 12, вип. 3 (19 листопада). — С. 177–209. — Bibcode:1971InMat..12..177R. — DOI:10.1007/BF01418780.
  • Lagarias J.C. Meyer's concept of quasicrystal and quasiregular sets // Commun. Math. Phys.. — 1996. — Т. 179, вип. 2 (19 листопада). — С. 356–376.
  • Moody R.V. Meyer sets and their duals // The Mathematics of Long Range Aperiodic Order, NATO ASI Series C. — 1997. — Т. 489 (19 листопада). — С. 403–441.
  • Chaim Goodman-Strauss. Matching rules and substitution tilings // Annals of Mathematics. — Annals of Mathematics, 1998. — Т. 147, вип. 1 (19 листопада). — С. 181–223. — DOI:10.2307/120988.
  • Chaim Goodman-Strauss. A small aperiodic set of planar tiles // European Journal of Combinatorics. — 1999. — Т. 20, вип. 5 (19 листопада). — С. 375–384. — DOI:10.1006/eujc.1998.0281.
  • Branko Grünbaum, Geoffrey C. Shephard.  — W.H. Freeman & Company, 1986. — ISBN 0-7167-1194-X.
  • Marjorie Senechal.  — Cambridge University Press, 1995. — ISBN 0-521-57541-9.
  • Socolar J.E.S. Simple octagonal and dodecagonal quasicrystals // Phys. Rev. B. — 1989. — Т. 39 (19 листопада). — С. 10519–51. — Bibcode:1989PhRvB..3910519S. — DOI:10.1103/PhysRevB.39.10519.
  • Penrose R. Remarks on Tiling: details of a 1 + ε + ε2-aperiodic set // The mathematics long range aperiodic order, NATO Adv. Sci. Inst. Ser. C. Math. Phys. Sci.. — 1997. — Т. 489 (19 листопада). — С. 467–497.
  • Nischke K.-P., Danzer L. A construction of inflation rules based on n-fold symmetry // Disc. and Comp. Geom.. — 1996. — Т. 15, вип. 2 (19 листопада). — С. 221–236. — DOI:10.1007/BF02717732.
  • Mozes S. Tilings, substitution systems and dynamical systems generated by them // Journal d'Analyse Mathématique. — 1989. — Т. 53, вип. 1 (19 листопада). — С. 139–186. — DOI:10.1007/BF02793412.
  • Charles Radin. The pinwheel tilings of the plane // Annals of Mathematics. — Annals of Mathematics, 1994. — Т. 139, вип. 3 (19 листопада). — С. 661–702. — DOI:10.2307/2118575.
  • de Bruijn N. G. Algebraic theory of Penrose's nonperiodic tilings of the plane, I, II // Nederl. Akad. Wetensch. Indag. Math.. — 1981. — Т. 43 (19 листопада). — С. 39–52, 53–66.
  • Le T.T.Q. Local rules for quasiperiodic tilings // The mathematics long range aperiodic order, NATO Adv. Sci. Inst. Ser. C. Math. Phys. Sci.. — 1997. — Т. 489 (19 листопада). — С. 331–366. — DOI:10.1007/978-94-015-8784-6_13.
  • Jarkko Kari. A small aperiodic set of Wang tiles // Discrete Mathematics. — 1996. — Т. 160, вип. 1–3 (19 листопада). — С. 259–264. — DOI:10.1016/0012-365X(95)00120-L.
  • Chaim Goodman-Strauss. A strongly aperiodic set of tiles in the hyperbolic plane // Inventiones Mathematicae. — 2005. — Т. 159, вип. 1 (19 листопада). — С. 119–132. — Bibcode:2004InMat.159..119G. — DOI:10.1007/s00222-004-0384-1.
  • Shahar Mozes. Aperiodic tilings // Inventiones Mathematicae. — 1997. — Т. 128, вип. 3 (19 листопада). — С. 603–611. — Bibcode:1997InMat.128..603M. — DOI:10.1007/s002220050153.
  • Block J., Weinberger S. Aperiodic tilings, positive scalar curvature and amenability of spaces // Journal of the AMS. — 1992. — Т. 5, вип. 4 (19 листопада). — С. 907–918. — DOI:10.1090/s0894-0347-1992-1145337-x.
  • Joshua Socolar. Weak matching rules for quasicrystals // Comm. Math. Phys.. — 1990. — Т. 129, вип. 3 (19 листопада). — С. 599–619. — Bibcode:1990CMaPh.129..599S. — DOI:10.1007/BF02097107.
  • Paul J. Steinhardt. A New Paradigm for the Structure of Quasicrystals. Архівовано з джерела 23 лютого 2007. Процитовано 2007-03-26.
  • Edwards W. S., Fauve S. Parametrically excited quasicrystalline surface waves // Physical Review E. — 1993. — Т. 47, вип. 2 (19 листопада). — С. R788 – R791.
  • Levy J-C. S., Mercier D. Stable quasicrystals // Acta Phys. Superficierum. — 2006. — Т. 8 (19 листопада). — С. 115.
  • Joshua E. S. Socolar1, Joan M. Taylor2. An aperiodic hexagonal tile // Journal of Combinatorial Theory Series A. — 2010. — 19 листопада. — arXiv:1003.4279v1.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.