Інтерференція хвиль
Інтерфере́нція хвиль (від лат. inter — взаємно, між собою; лат. ferio — вдаряю, вражаю) — явище накладання двох або більше когерентних хвиль, в результаті чого в одних місцях спостерігається підсилення кінцевої хвилі (інтерференційний максимум), а в інших місцях послаблення (інтерференційний мінімум).

Загальний опис
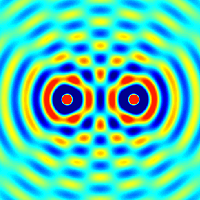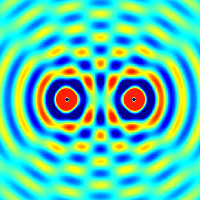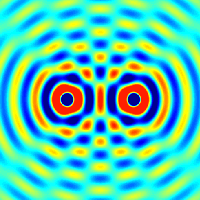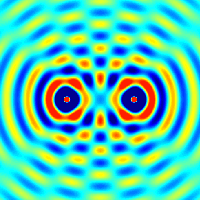
Інтерференція спостерігається у когерентних хвиль довільної природи — поверхневих (на воді), поперечних та поздовжніх звукових, електромагнітних (світло, радіохвилі), хвиль де Бройля.
При інтерференції результативне коливання є геометричною сумою коливань обох хвиль у відповідних точках. Цей принцип суперпозиції як правило є точним і порушується у окремих випадках, в деяких середовищах, коли амплітуда коливань є дуже високою (нелінійна оптика, нелінійна акустика).
Найпростішим випадком інтерференції є накладання двох гармонічних хвиль з однаковою частотою і поляризацією. В такому випадку результативна амплітуда А вираховується за формулою:
- ,
де та — амплітуди відповідних хвиль, — різниця фаз цих хвиль.
Використання
Явище інтерференції використовується, наприклад, в радіотехніці і акустиці для створення складних антен. Особливо велике значення інтерференція має в оптиці, вона лежить в основі оптичної та акустичної голографії.
Модель інтерференції немонохроматичних хвиль Захар'євського
Модель одновимірної хвилі
В загальному випадку одновимірну хвилю, що розповсюджується вздовж осі x, можна подати в такому вигляді:
- ,
де — змінна часу, — амплітуда коливання, — період коливань, — швидкість розповсюдження коливань вздовж осі x. Хвиля може також характеризуватися кутовою частотою:
- ,
де -довжина хвилі. Можна також ввести хвильовий вектор (число) у вигляді:
- .
Таким чином одномірну хвилю, що розповсюджується вздовж осі x можна також подати у вигляді:
- ,
де — фаза хвилі.
Модель інтерференції монохроматичної хвилі
Розглянемо монохроматичну хвилю з кутовою частотою , ширина якої рівна нулю
- .
В рамках моделі інтерференції Захар'євського[1] розглядаються дві хвилі, що розповсюджуються по двох шляхах інтерферометра:
Сумарну хвилю можна подати у вигляді:
- ,
де різниця фаз двох коливань буде:
- ,
де — різниця ходу двох хвиль. Для подальшого розгляду доцільно ввести нові змінні у вигляді:
- .
Тоді квадрат амплітуди сумарного коливання буде:
- .
Кути та пов'язані між собою таким чином:
- /
В результаті маємо наступне рівняння для інтерференційних коливань монохроматичної хвилі:
Оскільки енергія коливань залежить від квадрата амплітуди, тому для нас важливо з’ясувати можливі значення для різниці фаз та різниці ходу. Ми будемо мати два різні випадки.
В першому випадку ми маємо такі значення:
де — ціле позитивне або негативне число (порядок інтерференції). Максимальне значення квадрата модуля амплітуди тут буде:
- .
В другому випадку, коли ми маємо мінімальне значення квадрата амплітуди
ми будемо мати наступні значення для різниці фаз та різниці ходу:
- .
Часто буває, що амплітуди коливань є однакові . Тоді сумарна амплітуда буде:
її максимальне значення , а мінімальне — . Це найбільш бажаний результат, оскільки тут вся енергія коливань бере участь у створенні інтерференційної картини (найбільш різка контрастність).
Геометрична модель
Геометрична модель інтерференції базується на стандартній схемі, яка включає в себе два дзеркала Френеля[2], розміщені під невеликим кутом один до одного.
Інтервал між сусідніми світлими або темними смугами називається шириною смуги і позначається символом . Якщо -а смуга знаходиться від центру поля на відстані , то для неї різниця ходу рівна
- ,
де - відстань між двома когерентними джерелами світла, а - база інтерферометра (відстань між джерелами світла та площиною інтерференційного поля).
Для сусідньої -ї смуги, яка знаходиться від центру поля на відстані , маємо
- .
Очевидно, що різниця рівна ширині смуги, звідки знаходимо
- .
Таким чином, ширина смуги інтерференції хвиль з нульовою шириною лінії (), залежить від довжини хвиль,що (с-)падають.
Модель двох близьких частот
В природі не зустрічаються хвилі, які характеризуються однією частотою, без розширення частотного спектру (т.з. ширина лінії спектру хвилі). навіть у випадку лазерного променя ми маємо скінченне значення ширини лінії. В загальному випадку цей частотний спектр можна розглянути за допомогою двох близьких частот:
- .
Розглянемо дві близькі хвилі у вигляді:
- .
У випадку рівності амплітуд та фаз сумарне значення двох хвиль буде:
Середнє значення часто ми можемо розглядати як несучу частоту:
- ,
а різницю частот
як модуляційну частоту. Тут ми можемо також ввести поняття амплітуда модуляції
- .
Таким чином, сумарне значення модульованої хвилі буде
- .
Модель інтерференції зі скінченною шириною частотного спектру
Розглянемо випадок інтерференції двох модуляційних хвиль, які можна подати у вигляді:
- .
Тут враховано той факт, що несучі хвилі розповсюджуються вздовж осі , а модуляційні — вздовж осі . Кутові частоти тут будуть
- .
Хвильові вектори (числа) можна подати у вигляді:
- .
Оскільки , тому
- .
Таким чином, інтерференція двох модуляційних хвиль є типове двомірне явище в () — площині. Коефіцієнт модуляції двох хвиль визначається як:
- .
У випадку інтерференції його можна розглядати, як коефіцієнт підсилення двомірної інтерференції:
- .
Дві модуляційні хвилі можна подати у вигляді:
- .
де
а - різниця ходу вздовж осі . Сумарне значення інтерференційної хвилі тут буде:
Ми знову можемо скористатися заміною змінних у вигляді:
Це дає змогу переписати сумарну хвилю у вигляді:
де квадрат нової амплітуди та нова залежність між кутами буде:
Для інтерференції з модуляцією ми також будемо мати два випадки. В першому випадку ми маємо наступні значення для різниці фаз та різниці ходу:
де - ціле позитивне або негативне число (порядок інтерференції). Максимальне значення квадрата модуля амплітуди тут буде:
- .
В другому випадку, коли ми маємо мінімальне значення квадрата амплітуди
- ,
тоді будемо мати наступні значення для різниці фаз та різниці ходу:
- .
Геометрична модель модуляційної інтерференції
Основною умовою спостереження інтерференції модульованих хвиль є виконання співвідношення для модульованої різниці ходу:
- ,
а також співвідношення між ширинами смуг:
- .
Іншими словами, необхідна синхронність коливань вздовж осі з частотою та модуляційних коливань вздовж осі з частотою . Таким чином, для коефіцієнту модуляції (або коефіцієнту підсилення ширини смуги) маємо:
- .
Оскільки ми можемо спостерігати «підсилені» ширини смуг (декілька штук), то для їх створення необхідно дуже багато «непідсилених» смуг , а це означає що .
Безумовно, інтерференція немодульованих хвиль з частотою має пріоритет. Тому у випадку двох близьких частот різниця порядків інтерференції та повинна бути малим числом:
Тоді різниця ходу для двох близьких частот буде:
або
- .
Цей вираз також може переписати у формі:
- ,
де , а . Якщо як джерело світла взяти водневу лампу, для якої нм та нм, тоді
- ,
тобто не дуже велике число. Проте у випадку натрієвої лампи, де нм та нм, ми будемо мати велике число:
- .
Іншими словами, у випадку двох близьких ліній, наприклад, для лазерних променів з конечним значенням ширини спектру, або натрієвої лампи ми будемо мати великий коефіцієнт підсилення інтерференції модульованих хвиль . Проте, у випадку «білого світла» або водневої лампи коефіцієнт підсилення інтерференції буде малим . Таким чином, не залежно від конкретної схеми інтерферометра, інтерференція двох модульованих хвиль має велику ширину смуги:
при . Тому "зміщення ширини смуги" має вигляд:
- .
Очевидно, що мінімальне значення зміщення ширини смуги буде:
при . Точність вимірювання ширини модульованих хвиль буде, якщо не враховувати похибку телескопа чи мікроскопа:
де .
Див. також
Примітки
- Захарьевский А. Н. Интерферометры. — М. : Гос. изд. оборонной промышленности, 1952. — 296 с.
- Fresnel, Augustin «On the Action of Rays of Polarized Light upon Each Other», The Wave Theory of Light – Memoirs by Huygens, Young and Fresnel. — С. 79–156. — American Book Company, 1819.
Література
- Мала гірнича енциклопедія : у 3 т. / за ред. В. С. Білецького. — Д. : Донбас, 2004. — Т. 1 : А — К. — 640 с. — ISBN 966-7804-14-3.
- Романюк М. О., Крочук А. С., Пашук І. П. Оптика. — Л. : ЛНУ ім. Івана Франка, 2012. — 564 с.
- Ландсберг Г. С. Оптика. — М. : Физматлит, 2010. — 848 с.
- Сивухин Д. В. Оптика // Общий курс физики. — М. : Физматлит, 2006. — Т. 4. — 792 с.
