Верхня і нижня границі
В математичному аналізі верхня і нижня границі визначаються для числових послідовностей чи функцій і використовуються при їх вивченні. На відміну від звичайної границі, верхня і нижня границі завжди існують (хоч і можуть бути рівними нескінченності). Для нижньої границі послідовності використовуються позначення (поширене в українській і російській літературі) і (поширеніше в західній літературі). Для верхньої границі відповідні позначення мають вигляд і
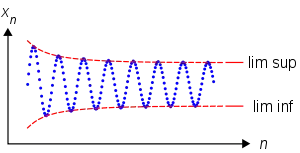
Визначення
Визначення для послідовностей
Нижню границю послідовності можна визначити:
або
Подібним чином верхня границя послідовності (xn) визначається
або
Визначення для функцій
Нехай дано дійсну функцію де і ξ — граничну точку I, тоді верхню і нижню границю функції в точці ξ можна визначити:
Аналогічно можна визначити односторонні границі функції в точці:
Приклади
Властивості
- У будь-якої послідовності існують верхня і нижня границі, що належать множині
- Числова послідовність збігається до тоді і тільки тоді, коли .
- Для будь-якого наперед узятого додатного числа всі елементи обмеженої числової послідовності , починаючи з деякого номера, залежного від , лежать усередині інтервалу .
- Якщо за межами інтервалу лежить лише скінченна кількість елементів обмеженої числової послідовності , то інтервал міститься в інтервалі .
- Виконуються нерівності:
Література
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Москва : Наука, 1966. — Т. 3. — 656 с.(рос.)
