Стичне коло

У диференціальній геометрії кривих, стичним колом достатньо гладкої плоскої кривої в даній точці р, на кривій, традиційно визначається як коло, що проходить через р і пару додаткових точок на цій кривій, які розташовані нескінченно близько до р. Центр кола знаходиться на внутрішній нормалі, а її кривина та ж сама, що і у даної кривої в цій точці. Тим самим радіус стичного кола визначається через кривину кривої: радіус дорівнює 1/k².

Стичне коло

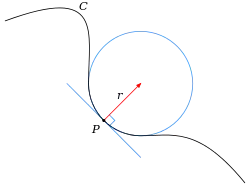
Одне з дотичних кіл, яке в заданій точці наближається до кривої найбільш щільно, було названо Лейбніцом «цілуючим колом» (лат. circulus osculans).

Центр і радіус стичного кола в даній точці називають центром кривини і радіусом кривини кривої в цій точці. Геометрична побудова була описана Ісааком Ньютоном у його Началах.

Опис у простих термінах

Уявіть собі автомобіль, що рухається по вигнутій дорозі по величезній плоскій площині. Раптом, в один прекрасний момент вздовж дороги, рульове колесо блокується в поточному положенні. Після цього автомобіль рухається по колу, яке «цілує» шлях авто в точці блокування. Кривина кола дорівнює, кривині дороги в цій точці. Це коло є стичним колом до кривої дороги в цій точці.

Математичний опис

Нехай γ(s) буде регулярною параметричною плоскою кривою, де s — довжина кривої, або натуральний параметр. Тоді можна визначити дотичний вектор T, одиничний вектор нормалі N, кривину k(s) і радіус кривини R(s) в кожній точці:

T(s)=\gamma '(s),\quad T'(s)=k(s)N(s),\quad R(s)={\frac {1}{\left|k(s)\right|}}.

Припустимо, що P — точка на γ, де k ≠ 0. Відповідний центр кривини точки Q на відстані R уздовж N в тому ж напрямку, якщо k є додатною, і в протилежному напрямку, якщо k від'ємна. Коло з центром у точці Q і радіусом R називається cтичним колом до кривої γ в точці P.

Якщо C є регулярною просторовою кривою, то стичне коло визначається аналогічним чином, використовуючи одиничний вектор нормалі N. Він лежить у стичній площині, яка натягнута на дотичний та головний нормальний вектор T і N в точці P.

Плоска крива також може бути надана в іншій регулярній параметризації $\gamma (t)\,=\,{\begin{pmatrix}x_{1}(t)\\x_{2}(t)\end{pmatrix}}\,$ де регулярність означає, що $\gamma '(t)\neq 0$ для усіх $t$ . Тоді формули для кривини k(t), одиничний вектор нормалі N(t), радіуса кривини R(t), і центру Q(t) дотичного кола будуть

k(t)={\frac {x_{1}'(t)\cdot x_{2}''(t)-x_{1}''(t)\cdot x_{2}'(t)}{{\Big (}x_{1}'(t)^{2}+x_{2}'(t)^{2}{\Big )}^{\frac {3}{2}}}}\qquad \qquad \qquad \qquad \qquad N(t)\,=\,{\frac {1}{||\gamma '(t)||}}\cdot {\begin{pmatrix}-x_{2}'(t)\\x_{1}'(t)\end{pmatrix}}

,

R(t)=\left|{\frac {{\Big (}x_{1}'(t)^{2}+x_{2}'(t)^{2}{\Big )}^{\frac {3}{2}}}{x_{1}'(t)\cdot x_{2}''(t)-x_{1}''(t)\cdot x_{2}'(t)}}\right|\qquad \qquad \mathrm {} \qquad \qquad Q(t)\,=\,\gamma (t)\,+\,{\frac {1}{k(t)\cdot ||\gamma '(t)||}}\cdot {\begin{pmatrix}-x_{2}'(t)\\x_{1}'(t)\end{pmatrix}}\,.

Властивості

Для кривої C, заданої достатньо гладкими параметричними рівняннями (двічі неперервно диференційованими), стичні кола можуть бути отримані в результаті граничного переходу: це межа послідовності кіл, що проходить через три різні точки на C, які наближаються до P.[1] Це повністю аналогічно побудові дотичної до кривої, як межі січних ліній через пари різних точок C, які наближаються до P.

Стичне коло S до плоскої кривої C в регулярній точці P може бути охарактеризоване такими властивостями:

Коло S проходить через точку P.
Коло S і крива C мають спільну дотичну в точці P, і тому у них спільна нормаль.
У околі точки P, відстань між точками кривої C та кола S в напрямку нормалі зменшується з кубічним або з більш високим ступенем відстані до P в дотичному напрямку.

Про це зазвичай кажуть, що «крива та її дотичне коло мають дотик третього або більш високого порядку» у точці P. Грубо кажучи, вектор-функції, що представляють C і S мають однакові значення разом зі своїми першими і другими похідними в точці P.

Якщо похідна кривини від s не дорівнює нулю в точці P, то тоді стичне коло перетинає криву C в точці P. Точки P, в яких похідна кривини дорівнює нулю, називаються вершинами. Якщо P є вершиною, то C та стичне коло мають дотик порядку, як мінімум, чотири. Якщо, крім того, кривина має ненульовий локальний максимум або мінімум в точці P, тоді стичне коло торкається кривої C в точці P, але не перетинає її.

Крива C може бути отримана як обгортка однопараметричного сімейства її стичних кіл. Їх центри, тобто центри кривини, утворюють іншу криву яка називається еволютою C. Вершини C відповідають особливим точкам на його еволюті.

Приклади

Парабола

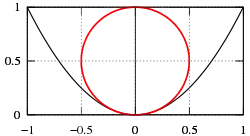
Стичне коло параболи у вершині має радіус 0.5 і дотик четвертого порядку.

Для параболи

\gamma (t)={\begin{pmatrix}t\\t^{2}\end{pmatrix}}

радіус кривини

R(t)=\left|{\frac {\left(1+4\cdot t^{2}\right)^{\frac {3}{2}}}{2}}\right|

У вершині $\gamma (0)={\begin{pmatrix}0\\0\end{pmatrix}}$ радіус кривини дорівнює R(0)=0.5 (див. малюнок). Парабола зі своїм стичним колом має дотик четвертого порядку . Для великих t радіус кривини збільшується ~ t³, тобто крива випрямляється все більше і більше.

Фігури Ліссажу

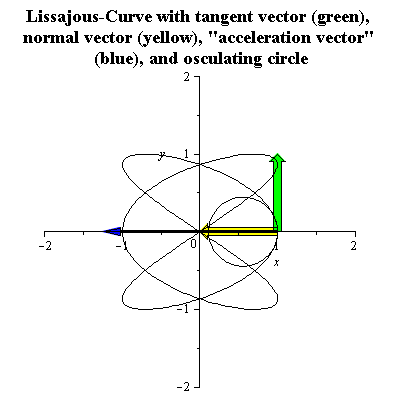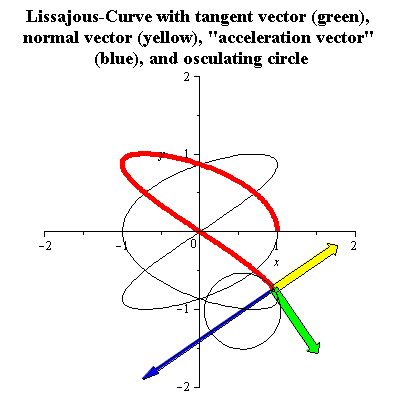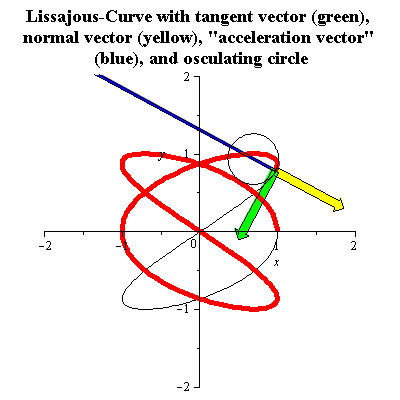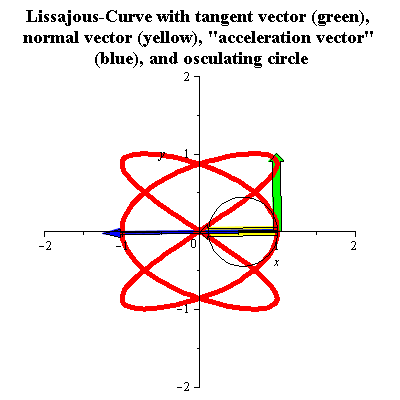
Animation of the osculating circle to a Lissajous curve

Фігури Ліссажу із співвідношенням частот (3:2) можуть бути параметризрвані таким чином

\gamma (t)\,=\,{\begin{pmatrix}\cos(3t)\\\sin(2t)\end{pmatrix}}\,.

Її знаковизначена кривина k(t), одиничний вектор нормалі N(t) і радіус кривини R(t), будуть

k(t)={\frac {6\cos(t)(8\cos(t)^{4}-10\cos(t)^{2}+5)}{(232\cos(t)^{4}-97\cos(t)^{2}+13-144\cos(t)^{6})^{3/2}}}\,,

N(t)\,=\,{\frac {1}{||\gamma '(t)||}}\cdot {\begin{pmatrix}-2\cos(2t)\\-3\sin(3t)\end{pmatrix}}

R(t)=\left|{\frac {(232\cos(t)^{4}-97\cos(t)^{2}+13-144\cos(t)^{6})^{3/2}}{6\cos(t)(8\cos(t)^{4}-10\cos(t)^{2}+5)}}\right|\,.

Дивіться малюнок анімації. «Вектор прискорення» буде другою похідною ${\frac {\mathrm {d} ^{2}\gamma (s)}{\mathrm {d} s^{2}}}$ від довжини кривої $s$ .

Примітки

Actually, point P plus two additional points, one on either side of P will do. See Lamb (on line): Horace Lamb (1897). An Elementary Course of Infinitesimal Calculus. University Press. с. 406.

Література

Деякі історичні нотатки по дослідженню кривих дивись

Grattan-Guinness & H. J. M. Bos (2000). From the Calculus to Set Theory 1630-1910: An Introductory History. Princeton University Press. с. 72. ISBN 0-691-07082-2.
Roy Porter, editor (2003). The Cambridge History of Science: v4 - Eighteenth Century Science. Cambridge University Press. с. 313. ISBN 0-521-57243-6.

Щодо застосування до їзди транспортних засобів дивись

JC Alexander and JH Maddocks: On the maneuvering of vehicles^{[недоступне посилання з травня 2019]}
Murray S. Klamkin (1990). Problems in Applied Mathematics: selections from SIAM review. Society for Industrial and Applied Mathematics. с. 1. ISBN 0-89871-259-9.

Посилання

Створіть власну анімацію стичних кіл (Maple-Worksheet)
Weisstein, Eric W. Стичне коло(англ.) на сайті Wolfram MathWorld.
Модуль по кривині

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Lamb-1] Actually, point P plus two additional points, one on either side of P will do. See Lamb (on line): Horace Lamb (1897). An Elementary Course of Infinitesimal Calculus. University Press. с. 406.