Дотик (математика)

В математиці, дві функції мають дотик порядку k, якщо вони мають однакове значення в точці Р, а також однакові похідні аж до порядку k. Це відношення еквівалентності, класи еквівалентності якого зазвичай називають струменем. Точки дотику також називають подвійним каспом.

Також можна казати, що криві та геометричні об'єкти, що мають в точці дотик k-го порядку, що є узагальненням поняття дотичної. Стичною кривою з даного сімейства кривих називається крива, яка має найвищий можливий порядок дотику із заданою кривою в даній точці; наприклад дотична пряма з сімейства ліній має перший порядок дотику із заданою кривою; стичне коло має другий порядок дотику, і т. д.[1]

Контактні форми є частковими диференціальними формами ступеня 1 на многовидах непарної вимірності (див. контактну геометрію). З контактними перетвореннями пов'язані перетворення координат, що мають важливе значення в класичній механіці. Див. також перетворення Лежандра.

Дотик між многовидами часто досліджують у теорії особливостей, де для класифікації типу дотику, розглядають A послідовності (A0: перетин, A1: дотична, A2: стична, …) і округлення або D-серії, де існує висока ступінь дотику зі сферою.

Дотик між кривими

Дві криві на площині, що перетинаються в точці p мають:

  • 1-точковий дотик якщо криві мають простий перетин (не по дотичній).
  • 2-точковий дотик якщо дві криві є дотичними.
  • 3-точки дотику, якщо кривина кривих рівна. Такі криві називаються стичними.
  • 4-точковим дотик, якщо похідні кривини рівні.
  • 5-точка дотику, якщо другі похідні кривини рівні.

Дотик між кривою і колом
Коло з 2-точковим контактом (дотичне)
Коло з 3-точковим контактом (стичне)
Коло з 4-точковим контактом на вершині кривої

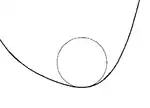
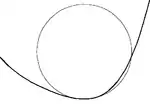
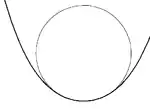
Для гладкої кривої S на площині, для кожної точки S(t) на кривій, завжди є рівно одне стичне коло, яке має радіус 1/κ(t), де k(t) — кривина кривої в точці t. Якщо крива має нульову кривину (тобто точка перегину на кривій), то дотичне коло буде являти собою пряму лінію. Набір центрів всіх дотичних кіл утворюють розгортку кривої.

Якщо похідна кривини κ'(t) дорівнює нулю, то дотичне коло буде мати 4-точковий контакт на кривій, у таких випадках кажуть, що крива має на вершину. Еволюта буде мати точку повернення в центрі кола. Знак другої похідної кривини визначає, чи має крива локальний мінімум або максимум кривини. Всі замкнуті криві будуть мати принаймні чотири вершини, два мінімуму і два максимуми (теорема про чотири вершини).

В цілому крива не буде мати 5-точковий дотик з колом. Однак, 5-точка дотику може виникнути у загальному 1-однопараметричну сімействі кривих, де дві вершини (один максимум і мінімум один) з'являються разом і зникають. В таких точках друга похідна кривини буде дорівнювати нулю.

Бі-дотичні в економетриці

В економетрії,бі-дотичними колами, можна вважати кола, які мають дві точки дотику з двома точками S(t1), S(t2) на кривій. Центри всіх Бі-дотичних кіл утворюють симетричну множину. Серединна вісь є підмножиною множини симетрій. Ці множини були використані як метод, що характеризує форми біологічних об'єктів Маріо Енріке Сімонсена, бразильського і англійського економетріста.

Посилання
  1. Rutter, J. W. (2000). Geometry of Curves. CRC Press. с. 174–175. ISBN 9781584881667..
  • Bruce, J. W.; P.J. Giblin (1992). Curves and Singularities. Cambridge. ISBN 0-521-42999-4.
  • Портеус Ян Р. (2001) Geometric Differentiation, pp 152—7, Cambridge University Press ISBN 0-521-00264-8 .
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.