Виявляння контурів
До виявля́ння ко́нтурів (англ. edge detection) належать різноманітні математичні методи, спрямовані на виявляння ко́нтурів (англ. edge), кривих у цифровому зображенні, на яких яскравість зображення змінюється різко, або, формальніше, має розриви. Аналогічна задача пошуку розривів в одновимірних сигналах відома як виявляння сходинок (англ. step detection), а задача знаходження розривів сигналу в часі відома як виявляння змін (англ. change detection). Виявляння контурів — один з основних інструментів в обробці зображень, машинному та комп'ютерному баченні, особливо в областях виявляння та виділяння ознак.[1]
| Виявляння ознак |
|---|
| Виявляння контурів |
| Виявляння кутів |
|
| Виявляння плям |
|
| Виявляння хребтів |
| Перетворення Гафа |
|
| Структурний тензор |
|
| Афінне інваріантне виявляння ознак |
|
| Опис ознак |
| Простір масштабів |
|
Обґрунтування
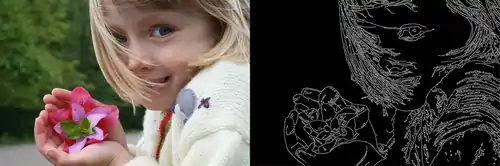
Метою виявляння різких змін яскравості зображення є фіксування важливих подій та змін у властивостях світу. Можливо показати, що за досить загальних припущень стосовно моделі формування зображення розриви яскравості зображення, ймовірно, відповідають:[2][3]
- розривам у глибині,
- розривам у спрямуванні поверхні,
- змінам у властивостях матеріалу та
- відхиленням в освітленні сцени.
В ідеальному випадку результатом застосування до зображення виявляння контурів може бути набір з'єднаних кривих, що позначують межі об'єктів, межі забарвлення поверхонь, а також усі криві, що відповідають розривам у спрямуванні поверхонь. Таким чином, застосування алгоритму виявляння контурів до зображення може значно зменшувати кількість даних, що підлягають обробці, й відтак може відфільтровувати інформацію, яку можна розцінювати як менш значущу, зберігаючи при цьому важливі структурні властивості зображення. Якщо крок виявляння контурів успішний, то подальшу задачу інтерпретування інформаційного вмісту первісного зображення може бути істотно спрощено. Проте отримувати такі ідеальні контури в картинах реального світу середньої складності можливо не завжди.
Контури, виділені з нетривіальних зображень, часто пошкоджено фрагментацією, що означає, що криві контурів не з'єднані, відсутні відрізки контурів, а також є хибні контури (англ. false edges), які не відповідають досліджуваному явищу в зображенні, що ускладнює подальшу задачу інтерпретування даних зображення.[4]
Виявляння контурів є одним з основних кроків в обробці зображень, аналізі зображень, розпізнаванні образів у зображеннях, та в методиках комп'ютерного бачення.
Властивості контурів
Контури, виділені з двовимірного зображення тривимірної сцени, можливо класифікувати як залежні від точки огляду (англ. viewpoint), або як незалежні від неї. Незалежний від точки огляду контур зазвичай відображає притаманні властивості тривимірних об'єктів, такі як забарвлення поверхні та її форма. Залежний від точки огляду контур може змінюватися за зміни точки огляду, і зазвичай відображає геометрію сцени, таку як затуляння одного об'єкту іншим.
Типовий контур може бути, наприклад, межею між областями червоного та жовтого кольорів. З іншого боку, лінія (яку може бути виділено виявлянням хребтів) може бути невеликою кількістю пікселів відмінного кольору на в іншому незмінному тлі. Тому зазвичай для лінії може бути по одному контуру з кожного з її боків.
Проста модель контуру
Хоча в певних працях розглядали виявляння ідеальних сходинкових контурів, контури, отримувані з природних зображень, зазвичай зовсім не є ідеальними сходинковими контурами. Натомість, вони зазвичай уражені одним або кількома з наступних явищ:
- фокусним розмиттям, спричинюваним скінченною глибиною різкості та скінченною функцією розсіювання точки.
- напівтіньовим розмиттям, викликаним тінями, створюваними джерелами світла ненульового радіусу.
- затіненням на гладенькому об'єкті
Як найпростіше розширення ідеальної моделі сходинкового контуру для моделювання ефектів розмиття контурів у практичних застосуваннях багато дослідників використовували гауссово згладжений сходинковий контур (функцію похибки).[4][5] Таким чином, одновимірне зображення , що має рівно один контур, розташований в , можна моделювати як
Ліворуч від контуру яскравість , а праворуч від контуру — . Масштабний коефіцієнт називають масштабом розмиття контуру. В ідеалі цей параметр масштабу слід налаштувати відповідно до якості зображення, щоб уникати руйнування істинних контурів у ньому.[джерело?]
Чому це нетривіальне завдання
Щоби проілюструвати, чому виявляння контурів не є тривіальним завданням, розгляньмо задачу виявлення контурів у наступному одновимірному сигналі. Тут ми можемо інтуїтивно сказати, що має бути контур між 4-м та 5-м пікселями.
| 5 | 7 | 6 | 4 | 152 | 148 | 149 |
Якби різниця яскравості між 4-м та 5-м пікселями була нижчою, а різниці яскравості між сусідніми прилеглими пікселями — вищими, то було би не так легко сказати, що у відповідній області має бути контур. Понад те, можливо було би стверджувати, що це випадок, у якому є декілька контурів.
| 5 | 7 | 6 | 41 | 113 | 148 | 149 |
Отже, чітко вказати певний поріг того, наскільки великою має бути зміна яскравості між двома сусідніми пікселями, щоби ми могли сказати, що між цими пікселями має бути контур, не завжди просто.[4] Справді, це одна з причин, чому виявляння контурів може бути нетривіальною задачею, якщо тільки об'єкти в сцені не дуже прості, а умови освітлення можливо добре контролювати (див., наприклад, контури, виділені в зображенні з дівчинкою вище).
Підходи
Існує багато методів виявляння контурів, але більшість із них можливо згрупувати у дві категорії: на основі пошуку, та на основі перетину нуля. Методи на основі пошуку виявляють контури, спочатку обчислюючи міру вираженості контуру (англ. edge strength), як правило, як вираження першої похідної, таке як величина градієнта, а потім шукають локальні напрямні максимуми величини градієнта з використанням обчисленої оцінки локального спрямування контуру, зазвичай, напряму градієнта. Методи на основі перетину нуля, щоби знаходити контури, шукають перетини нуля вираженням другої похідної, обчисленим із зображення, зазвичай, перетини нуля лапласіаном, або перетини нуля нелінійним диференціальним виразом. Як етап попередньої обробки для виявляння контурів майже завжди застосовують етап згладжування, як правило, гауссового (див. також знижування шуму).
Опубліковані методи виявляння контурів переважно відрізняються типами застосовуваних фільтрів згладжування та способами обчислення міри вираженості контуру. Оскільки багато методів виявляння контурів покладаються на обчислення градієнтів зображення, вони також відрізняються типами фільтрів, застосовуваних для обчислення оцінок градієнта в напрямах x та y.
Огляд низки різних методів виявляння контурів є в (Ziou and Tabbone 1998);[6] див. також енциклопедичні статті про виявляння контурів в «Енциклопедії з математики»[3] та «Енциклопедії з інформатики та інженерії».[7]
Кенні
Джон Кенні розглядав математичну задачу виведення оптимального згладжувального фільтра за заданого критерію виявляння, локалізації та мінімізації множинних відгуків на один контур.[8] Він показав, що оптимальним фільтром за цих припущень є сума чотирьох експоненційних доданків. Він також показав, що цей фільтр можливо добре наблизити першими похідними гауссіанів. Кенні також ввів поняття пригнічування немаксимумів (англ. non-maximum suppression), яке означає, що, за заданих фільтрів попереднього згладжування, точки контурів визначаються як точки, в яких величина градієнта набуває локального максимуму в напрямі градієнта. Шукати перетин нуля другою похідною вздовж напряму градієнта вперше запропонував Гаралік.[9] Знадобилося менше двох десятиліть, щоби знайти сучасне геометричне варіаційне значення для цього оператора, яке пов'язує його з алгоритмом Марра — Гілдрета виявляння контурів (перетин нуля лапласіаном). Це спостереження було представлено Роном Кіммелом та Альфредом Брукштайном.[10]
Хоча його працю й було зроблено на початку часів комп'ютерного бачення, алгоритм Кенні виявляння контурів (включно з його різновидами) все ще перебуває на рівні останніх досягнень.[11] Алгоритми виявляння контурів, які працюють краще за алгоритм Кенні, зазвичай вимагають більшого обчислювального часу, або більшої кількості параметрів.
Алгоритм Кенні — Деріша було виведено на основі подібних математичних критеріїв, що й алгоритм Кенні, але починаючи з дискретної точки зору, а потім ведучи до набору рекурсивних фільтрів для згладжування зображення замість експоненційних або гауссових фільтрів.[12]
Описаний нижче диференціальний алгоритм виявляння контурів можливо розглядати як переформулювання методу Кенні з точки зору диференціальних інваріантів, обчислюваних з масштабно-просторового подання, що дає низку переваг з погляду як теоретичного аналізу, так і субпіксельного втілення. У цьому аспекті було показано, що добрим вибором для виділяння меж у природних сценах є логарифмічний фільтр Ґабора.[13]
Інші методи першого порядку
Для оцінки градієнтів зображення на основі вхідного зображення або його згладженої версії можливо застосовувати різні оператори градієнта. Найпростіший підхід — використовувати центральні різниці:
що відповідає застосуванню до даних зображення наступних фільтрових масок:
Добре відомий і більш ранній оператор Собеля ґрунтується на наступних фільтрах:
За таких оцінок перших похідних зображення величину градієнту відтак обчислюють через
а спрямування градієнта можливо оцінювати через
Інші різницеві оператори першого порядку для оцінювання градієнта зображення було запропоновано в операторі Прюітт, хресті Робертса, операторі Каялі[14] та операторі Фрая — Чена.
Розмір фільтрів можливо розширювати задля уникання проблеми з розпізнаванням контурів у зображеннях із низьким ССШ. Ціною цієї операції є втрати з точки зору роздільності. Прикладом є розширений оператор Прюітт 7×7.
Порогування та зв'язування
Щойно ми обчислили міру вираженості контуру (зазвичай, величину градієнта), наступним етапом є застосування порогу, щоби вирішити, чи присутні контури в якісь точці зображення. Що нижчий поріг, то більше контурів буде виявлено, й результат буде все вразливішим для шуму та виявляння контурів недоречних особливостей зображення. І навпаки, високий поріг може пропускати ледь вловимі контури, або давати в результаті фрагментовані контури.
Якщо контур застосовувати лише до зображення величини градієнту, то отримувані контури загалом будуть товстими, й потрібна якась подальша обробка для їхнього витоншування. Проте для контурів, виявляних із придушуванням немаксимумів, криві контурів є тонкими за визначенням, і пікселі контурів можливо зв'язувати в контурний багатокутник за допомогою процедури зв'язування контурів (англ. edge linking, простежування контурів, англ. edge tracking). На дискретній ґратці етап придушування немаксимумів можливо втілювати оцінюванням напряму градієнта за допомогою перших похідних, наступним округлюванням напряму градієнта до кратних 45 градусів, і, зрештою, порівнюванням значень величини градієнта в оціненому напрямі градієнта.
Для розв'язання проблеми відповідних порогів зазвичай використовують підхід порогування з гістерезисом. Цей метод використовує для пошуку контурів роздвоєні пороги. Ми починаємо із застосування верхнього порогу для пошуку початку контуру. Щойно ми знайшли початкову точку, ми простежуємо шлях контуру зображенням піксель за пікселем, позначуючи контур, де ми перебуваємо вище за нижній поріг. Ми припиняємо позначувати наш контур лише тоді, коли значення падає нижче нашого нижнього порогу. Цей підхід спирається на припущення, що контури переважно перебувають у безперервних кривих, і дозволяє нам простежувати слабку ділянку контуру, який ми бачили раніше, без того, щоби позначувати контуром кожен піксель із шумом у зображенні. Проте ми все одно маємо проблему з обиранням відповідних порогових параметрів, і придатні порогові значення можуть різнитися в різних частинах зображення.
Витоншування контурів
Витоншування контурів (англ. edge thinning) — це методика, яку використовують для усування небажаних паразитних точок на контурах у зображенні. Цю методику застосовують після відфільтровування шуму з зображення (за допомогою медіанного, гауссового фільтра тощо), застосування оператора контурів (подібного до описаних вище, Кенні або Собеля) для виявляння контурів, і після згладжування контурів із застосуванням відповідного порогового значення. Воно видаляє всі небажані точки, і, якщо застосовувати його обачно, в результаті утворюються елементи контурів товщиною в один піксель.
Переваги:
- Рівні та тонкі контури сприяють кращій продуктивності розпізнавання об'єктів.
- Якщо застосовують перетворення Гафа для виявляння ліній та еліпсів, то витоншування може давати набагато кращі результати.
- Якщо контур виявляється межею області, то витоншування може легко, без особливої алгебри, давати параметри її зображення, як-от периметр.
Для цього використовують багато популярних алгоритмів, один з яких описано нижче:
- Обрати тип зв'язності, як-то 8, 6 або 4.
- Перевагу віддають 8-зв'язності, за якої розглядають усі безпосередні пікселі, що оточують заданий.
- Вилучити точки з півночі, півдня, сходу та заходу.
- Зробити це за кілька проходів, тобто, після проходу для півночі використати те саме напівоброблене зображення в іншому проході, й так далі.
- Вилучати точку, якщо:
Точка не має сусідів на півночі (у проході для півночі, й на відповідних напрямках для інших проходів).
Точка не є кінцем лінії.
Точка ізольована.
Вилучання точок жодним чином не призведе до роз'єднання їхніх сусідів. - Інакше лишити точку.
Кількість проходів за напрямом слід обирати відповідно до бажаного рівня точності.
Підходи другого порядку
Деякі оператори виявляння контурів натомість ґрунтуються на других похідних яскравості. Це, по суті, вловлює темп зміни градієнта яскравості. Таким чином, в ідеальному неперервному випадку виявляння перетинів нуля другою похідною вловлює локальні максимуми градієнту.
Ранній оператор Марра — Гілдрета ґрунтується на виявлянні перетинів нуля оператором Лапласа, застосованого до гауссово згладженого зображення. Проте можливо показати, що цей оператор також повертатиме хибні контури, що відповідають локальним мінімумам величини градієнта. Більше того, цей оператор даватиме погану локалізацію на вигнутих контурах. Отже, цей оператор становить сьогодні переважно історичний інтерес.
Диференціальний
Досконаліший підхід другого порядку до виявляння контурів, який автоматично виявляє контури з субпіксельною точністю, використовує для виявляння перетинів нуля другою напрямною похідною в напрямі градієнта наступний диференціальний підхід:
Дотримуючись диференціального геометричного способу вираження вимоги придушування немаксимумів, запропонованого Ліндебергом,[4][15] введімо в кожній точці зображення локальну систему координат , -напрям якої паралельний напряму градієнта. Виходячи з припущення, що зображення було попередньо згладжено гауссовим згладжуванням, та було обчислено масштабно-просторове подання в масштабі , ми можемо вимагати, щоби величина градієнта масштабно-просторового подання, яка дорівнює першій напрямній похідній у -напрямі , мала у -напрямі нульову першу напрямну похідну
тоді як друга напрямна похідна у -напрямі повинна бути від'ємною, тобто,
Записане як явний вираз у термінах локальних частинних похідних , це визначення контуру можливо виразити як перетин нуля кривими диференціального інваріанта
що задовольняє умову для знаку на наступному диференціальному інваріанті
- ,
де позначують частинні похідні, обчислені з масштабно-просторового подання , отриманого згладжуванням первинного зображення гауссовим ядром. Таким чином, контури автоматично отримуватимуться як неперервні криві з субпіксельною точністю. До цих диференціальних і субпіксельних сегментів контурів також можливо застосовувати гістерезисне порогування.
На практиці наближення перших похідних можливо обчислювати за допомогою центральних різниць, як описано вище, тоді як другі похідні можливо обчислювати з масштабно-просторового подання відповідно до:
що відповідає таким маскам фільтрів:
Вищі похідні для умови третього порядку для знаку можливо отримувати аналогічно.
На основі фазової конгруентності
Недавній розвиток методів виявляння контурів для пошуку місць їхнього розташування використовує підхід частотної області. Методи фазової конгруентності (відомої також як фазова когерентність) намагаються знаходити місця на зображенні, де всі синусоїди в частотній області синфазні. Ці місця загалом відповідатимуть розташуванню того, що сприймається як контур, незалежно від того, чи цей контур являє собою велику зміну яскравості в просторовій області. Ключова перевага цієї методики полягає в тому, що вона добре реагує на махові смуги й уникає хибних спрацьовувань, які зазвичай трапляються навколо дахових контурів. Даховий контур (англ. roof edge) — це розрив у першій похідній профілю яскравості.[16]
Фазоворозтягувальне перетворення

Фазоворозтягувальне перетворення, або ФРП (англ. phase stretch transform, PST) — це навіяний фізикою обчислювальний підхід до обробки сигналів та зображень. Однією з його корисних властивостей є виявляння та класифікування ознак.[17][18] ФРП це похідний продукт дослідження дисперсійного перетворення Фур’є з розтягуванням у часі. ФРП перетворює зображення, моделюючи поширення дифракційним середовищем зі сконструйованою тривимірною дисперсійною властивістю (показником заломлення). Ця операція покладається на симетричність дисперсійного профілю, і її можливо розуміти в термінах дисперсійних власних функцій або режимів розтягування.[19] ФРП виконує подібні функції, що й фазовоконтрастна мікроскопія, але на цифрових зображеннях. ФРП застосовне як до цифрових зображень, так і до часових даних, даних часових рядів.
Субпіксельні
Для підвищення точності виявляння контурів було запропоновано декілька субпіксельних методик, включно з методами допасовування кривої (англ. curve-fitting), на основі моменту (англ. moment-based),[20][21] відбудовними (англ. reconstructive) методами, та методами ефекту часткової площі (англ. partial area effect methods).[22] Ці методи мають різні характеристики. Методи допасовування кривих обчислювально прості, але на них легко впливає шум. Методи на основі моменту використовують інтегральний підхід для зменшення впливу шуму, але в деяких випадках можуть вимагати більше обчислень. Відбудовні методи використовують горизонтальні та вертикальні градієнти для побудови кривої та знаходження піку кривої як субпіксельного контуру. Методи ефекту часткової площі ґрунтуються на гіпотезі, що значення кожного пікселя залежить від площі по обидві сторони контуру всередині цього пікселя, що забезпечує точну індивідуальну оцінку для кожного пікселя контуру. Деякі варіанти методики на основі моменту виявилися найточнішими для ізольованих контурів.[21]
Див. також
- Згортка (математичний аналіз) § Застосування
- Фільтрування зі зберіганням контурів
- Виявляння ознак (комп'ютерне бачення) про інші низькорівневі виявлячі ознак
- Похідна зображення
- Фільтр Ґабора
- Знижування шуму в зображеннях
- Оператор Кірша для виявляння контурів у компасних напрямах
- Виявляння хребтів про зв'язок між виявлянням контурів та виявлянням хребтів
- Логарифмічний фільтр Ґабора
- Фазоворозтягувальне перетворення
Примітки
- Umbaugh, Scott E (2010). Digital image processing and analysis : human and computer vision applications with CVIPtools (вид. 2nd). Boca Raton, FL: CRC Press. ISBN 978-1-4398-0205-2. (англ.)
- H.G. Barrow and J.M. Tenenbaum (1981) "Interpreting line drawings as three-dimensional surfaces", Artificial Intelligence, vol 17, issues 1–3, pages 75–116. (англ.)
- Lindeberg, Tony (2001). Edge detection. У Hazewinkel, Michiel. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4. (англ.)
- T. Lindeberg (1998) "Edge detection and ridge detection with automatic scale selection", International Journal of Computer Vision, 30, 2, pages 117–154. (англ.)
- W. Zhang and F. Bergholm (1997) "Multi-scale blur estimation and edge type classification for scene analysis", International Journal of Computer Vision, vol 24, issue 3, Pages: 219–250. (англ.)
- D. Ziou and S. Tabbone (1998) "Edge detection techniques: An overview", International Journal of Pattern Recognition and Image Analysis, 8(4):537–559, 1998 (англ.)
- J. M. Park and Y. Lu (2008) "Edge detection in grayscale, color, and range images", in B. W. Wah (editor) Encyclopedia of Computer Science and Engineering, doi 10.1002/9780470050118.ecse603 (англ.)
- J. Canny (1986) "A computational approach to edge detection", IEEE Transactions on Pattern Analysis and Machine Intelligence, vol 8, pages 679–714. (англ.)
- R. Haralick, (1984) "Digital step edges from zero crossing of second directional derivatives", IEEE Transactions on Pattern Analysis and Machine Intelligence, 6(1):58–68. (англ.)
- R. Kimmel and A.M. Bruckstein (2003) "On regularized Laplacian zero crossings and other optimal edge integrators", International Journal of Computer Vision, 53(3) pages 225–243. (англ.)
- Shapiro L. G. & Stockman G. C. (2001) Computer Vision. London etc.: Prentice Hall, Page 326. (англ.)
- R. Deriche (1987) Using Canny's criteria to derive an optimal edge detector recursively implemented, Int. J. Computer Vision, vol 1, pages 167–187. (англ.)
- Sylvain Fischer, Rafael Redondo, Laurent Perrinet, Gabriel Cristobal. Sparse approximation of images inspired from the functional architecture of the primary visual areas. EURASIP Journal on Advances in Signal Processing, special issue on Image Perception, 2007 (англ.)
- Dim, Jules R.; Takamura, Tamio (11 грудня 2013). Alternative Approach for Satellite Cloud Classification: Edge Gradient Application. Advances in Meteorology (англ.) 2013: 1–8. ISSN 1687-9309. doi:10.1155/2013/584816. Проігноровано невідомий параметр
|doi-access=(довідка) (англ.) - T. Lindeberg (1993) "Discrete derivative approximations with scale-space properties: A basis for low-level feature extraction", J. of Mathematical Imaging and Vision, 3(4), pages 349–376. (англ.)
- T. Pajdla and V. Hlavac (1993) "Surface discontinuities in range images, " in Proc IEEE 4th Int. Conf. Comput. Vision, pp. 524–528. (англ.)
- M. H. Asghari, and B. Jalali, "Edge detection in digital images using dispersive phase stretch, " International Journal of Biomedical Imaging, Vol. 2015, Article ID 687819, pp. 1–6 (2015). (англ.)
- M. H. Asghari, and B. Jalali, "Physics-inspired image edge detection, " IEEE Global Signal and Information Processing Symposium (GlobalSIP 2014), paper: WdBD-L.1, Atlanta, December 2014. (англ.)
- B. Jalali and A. Mahjoubfar, "Tailoring Wideband Signals With a Photonic Hardware Accelerator, " Proceedings of the IEEE, Vol. 103, No. 7, pp. 1071–1086 (2015). (англ.)
- Ghosal, S.; Mehrota, R (1 січня 1993). Orthogonal Moment Operators for Subpixel Edge Detection. Pattern Recognition 26 (2): 295–306. doi:10.1016/0031-3203(93)90038-X. (англ.)
- Christian, John (1 січня 2017). Accurate Planetary Limb Localization for Image-Based Spacecraft Navigation. Journal of Spacecraft and Rockets 54 (3): 708–730. Bibcode:2017JSpRo..54..708C. doi:10.2514/1.A33692. (англ.)
- Trujillo-Pino, Agustín; Krissian, Karl; Alemán-Flores, Miguel; Santana-Cedrés, Daniel (1 січня 2013). Accurate subpixel edge location based on partial area effect. Image and Vision Computing 31 (1): 72–90. doi:10.1016/j.imavis.2012.10.005. Проігноровано невідомий параметр
|hdl-access=(довідка) (англ.)
Література
- Lindeberg, Tony (2001). Edge detection. У Hazewinkel, Michiel. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4. (англ.)
- Розділ про виявляння контурів в «Енциклопедії з інформатики та інженерії» (англ.)
- Виявляння контурів із застосуванням ПКВМ (англ.)
- Виявляння відрізків прямих a-contrario, з кодом та інтерактивною демонстрацією (англ.)
- Виявляння контурів із застосуванням MATLAB (англ.)
- Субпіксельне виявляння контурів із застосуванням MATLAB (англ.)
