Згортка (математичний аналіз)
Зго́ртка (англ. convolution) — математична операція двох функцій та , що дозволяє отримати третю функцію:
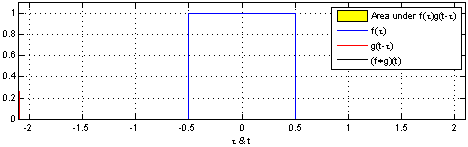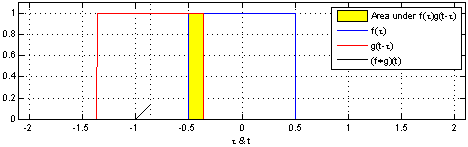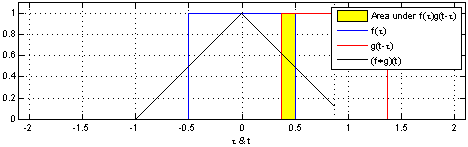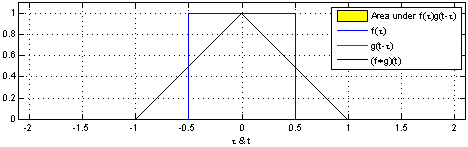
Згортка двох квадратних імпульсів: результатом є імпульс трикутної форми. Одна з функцій (в даному випадку g) спочатку відображається черезз і тоді зсувається на t, результатом є . Площа під кривою, що є добутком цих фунцій і є згорткою по t. Горизонтальна вісь це для f і g, і t для
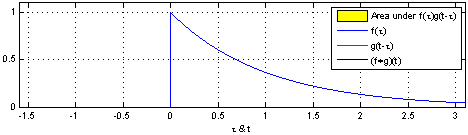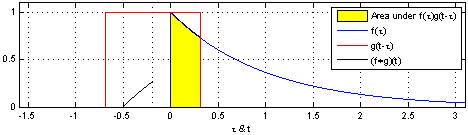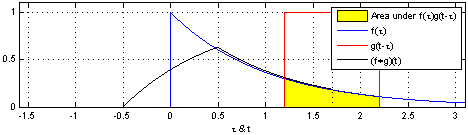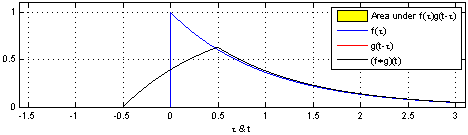
Згортка квадратного імпульсу (вхідний сигнал) з імпульсом відповіді в RC колі для отримання кривої вихідного сигналу. Інтеграл добутку — це площа жовтої ділянки.
Основною властивістю згортки є те, що фур'є-образ згортки пропорційний добутку фур'є-образів функцій.
Згортка на групах
Нехай — група Лі, оснащена мірою Хаара , і — дві функції, визначенні на . Тоді їх згорткою називається функція
- .
Властивості
- Лінійність (дистрибутивність щодо додавання і асоціативність добутку з скаляром):
- Правило диференціювання:
де означає похідну функції .
де означає перетворення Фур'є функції.
Якщо є матрицею дискретного перетворення Фур'є, то
,
де — символ торцевого добутку матриць[1][2][3][4][5], означає добуток Кронекера, — символ добутку Адамара (тотожність є розвитком властивості відлікового скетча[6]).
Застосування

Гаусове розмиття може використовуватись щоб отримати гладке монохромне зображення з півтонового друку
Згортки та пов'язані операції знаходять багато застосувань в науці, інженерії та математиці.
- В обробці зображень:
- Згортка в обробці зображень використовується в багатьох фільтрах, наприклад для розмиття, чи виявлення контурів.
- В фотографії, несфокусована фотографія є згорткою чіткого зображення з функцією лінзи. Фотографічний термін для цього поняття — Боке.
- В статистиці, зважене рухоме середнє є згорткою.
- Згорткові нейронні мережі застосовують багато каскадів ядер згорток для застосування в областях комп'ютерного зору та штучного інтелекту
Приклад програми
Нижче наведено приклад згортки, написаний на С++ :
/*
* Розмір вихідної послідовності рівний M + N - 1
*/
double * conv(double * x, int N, double * h, int M)
{
double * result = new double[N + M - 1];
memset(result, 0, sizeof(double) * (N + M - 1));
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < M; ++j)
{
result[i + j] += x[i] * h[j];
}
}
return result;
}
Див. також
Примітки
- Slyusar, V. I. (27 грудня 1996). End products in matrices in radar applications.. Radioelectronics and Communications Systems.– 1998, Vol. 41; Number 3: 50–53.
- Slyusar, V. I. (20 травня 1997). Analytical model of the digital antenna array on a basis of face-splitting matrix products.. Proc. ICATT-97, Kyiv: 108–109.
- Slyusar, V. I. (15 вересня 1997). New operations of matrices product for applications of radars. Proc. Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED-97), Lviv.: 73–74.
- Slyusar, V. I. (13 березня 1998). A Family of Face Products of Matrices and its Properties. Cybernetics and Systems Analysis C/C of Kibernetika I Sistemnyi Analiz.- 1999. 35 (3): 379–384. doi:10.1007/BF02733426.
- Slyusar, V. I. (2003). Generalized face-products of matrices in models of digital antenna arrays with nonidentical channels. Radioelectronics and Communications Systems 46 (10): 9–17.
- Ninh, Pham; Rasmus, Pagh (2013). Fast and scalable polynomial kernels via explicit feature maps SIGKDD international conference on Knowledge discovery and data mining. Association for Computing Machinery. doi:10.1145/2487575.2487591.
Література
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — 4-е изд. — Москва : Наука, 1976. — 544 с. — ISBN 5-9221-0266-4.(рос.)
- Ширяев А. Н. Вероятность, — М.: Наука. 1989.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
