Внутрішня точка
Внутрішня точка, у топології — це точка, яка входить у дану множину разом з деяким своїм околом.
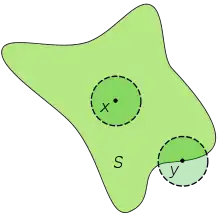
Точка Х є внутрішньою для множини S, а точка У — ні, оскільки будь-який її окіл виходить за межі множини S.
Інтуїтивно внутрішня точка - це точка, яка не перебуває на краю.
Визначення
Нехай — топологічний простір з топологією , і . Точка є внутрішньою для тоді і тільки тоді, коли існує відкрита множина , така що та .
Зауваження
- З визначення відразу виходить, що у відкритій множині всі точки внутрішні.
- Також вірно і зворотне: множина, всі точки якої внутрішні, є відкритою.
Окремі випадки
У метричному просторі визначення внутрішньої точки приймає наступний вигляд. Хай X — метричний простір з метрикою d, і M — його підмножина. Точка є внутрішньою для M тоді і тільки тоді, коли існує , таке що . Інакше кажучи, x входить в M разом з кулею радіусу з центром в x.
Дивись також
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
