Вузол (інформатика)

Вузол є основною одиницею, яка використовується в обчислювальній техніці. Вузли — це пристрої або точки даних на великій мережі. Пристрої, такі як персональний комп'ютер, стільниковий телефон або принтер, є вузлами. При визначенні вузлів в Інтернеті вузлом є все, що має IP-адресу. Вузли — це окремі частини більшої структури даних, такі, як зв'язані списки та дерева даних. Вузли містять дані, а також можуть посилатися на інші вузли. Зв'язки між вузлами часто реалізуються покажчиками.

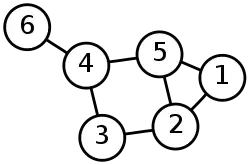
У теорії графів зображення забезпечує спрощений перегляд мережі, де кожен з чисел являє собою інший вузол.

Вузли та дерева
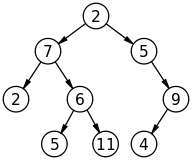
Просте двійкове дерево двійкове дерево розміром 9 і висотою 3, з кореневим вузлом, значення якого дорівнює 2. Наведене вище дерево незбалансоване і не відсортоване.

Вузли часто розташовуються на деревоподібних структурах. Вузол являє собою інформацію, що міститься в єдиній структурі даних. Ці вузли можуть містити значення або умову, або, можливо, служити іншою незалежною структурою даних. Вузли представлені одним батьківським вузлом. Найвища точка на деревній структурі називається кореневим вузлом, який не має батьківського вузла, але служить батьківським або «прабатьківським» для всіх вузлів під ним у дереві. Висота вузла визначається загальною кількістю ребер на шляху від цього вузла до останнього вузла листа, а висота дерева дорівнює висоті кореневого вузла.[1] Глибина вузла визначається відстанню між цим вузлом й кореневим вузлом. Кореневий вузол має глибину нуля.[2] Дані можуть бути виявлені вздовж цих мережевих шляхів.[3] IP-адреса використовує цю систему вузлів для визначення свого розташування в мережі.

Визначення
  • Дочірній: дочірній вузол — це вузол, що проходить від іншого вузла. Наприклад, комп'ютер з доступом до Інтернету можна вважати дочірнім вузлом вузла, що представляє Інтернет. Зворотне співвідношення є відношенням батьківського вузла. Якщо вузол C є дочірнім вузлом A, то A є батьківським вузлом C.
  • Ступінь: ступінь вузла — число дітей вузла.
  • Глибина: глибина вузла A — це довжина шляху від A до кореневого вузла. Кажуть, що кореневий вузол має глибину 0.
  • Край: зв'язок між вузлами.
  • Ліс: набір дерев.
  • Висота: висота вузла A — це довжина найдовшого шляху через дітей до листового вузла.
  • Внутрішній вузол: вузол з принаймні однією дитиною.
  • Кінцевий вузол: вузол без дочірніх елементів.
  • Кореневий вузол: вузол, що відрізняється від інших вузлів дерева. Зазвичай вона зображена як найвищий вузол дерева.
  • Вузли сімейства: це вузли, підключені до одного батьківського вузла.

Мови розмітки

Інше поширене використання дерев вузлів у веб розробці. У програмуванні XML використовується для передачі інформації між комп'ютерними програмістами та комп'ютерами. З цієї причини XML використовується для створення спільних протоколів зв'язку, що використовуються в офісному програмному забезпеченні, та служить базою для розробки сучасних мов розмітки в Інтернеті, таких як XHTML. Хоча подібні до того, як до нього звертаються програмісти, HTML та CSS, зазвичай це мова, яка використовується для розробки тексту та дизайну вебсайту. У той час як XML, HTML і XHTML надають мову і вираз, DOM виконує роль перекладача.[4]

Тип вузла

Різні типи вузлів у дереві представлені специфічними інтерфейсами. Іншими словами, тип вузла визначається тим, як він взаємодіє з іншими вузлами. Кожен вузол має властивість типу вузла, що визначає тип вузла, наприклад, однорівневий або листовий.

Наприклад, якщо властивість типу вузла є властивістю константи для вузла, це властивість визначає тип вузла. Тому, якщо властивість типу вузла є постійним вузлом ELEMENT_NODE, можна знати, що цей вузол є елементом об'єкта. Цей об'єкт використовує інтерфейс Element для визначення всіх методів і властивостей цього конкретного вузла. Типи вузлів

Різні типи та описи вузлів Консорціум Всесвітньої павутини:

  • Document представляє весь документ (кореневий вузол дерева DOM)
  • DocumentFragment являє собою «легкий» об'єкт Document, який може містити частину документа
  • DocumentType надає інтерфейс для об'єктів, визначених для документа
  • ProcessingInstruction являє собою інструкцію обробки
  • EntityReference являє собою посилання на сутність
  • Element являє собою елемент
  • Attr являє собою атрибут
  • Text являє собою текстовий вміст елемента або атрибута
  • CDATASection являє собою розділ CDATA у документі (текст, який НЕ буде аналізуватися синтаксичним аналізатором)
  • Comment представляє коментар
  • Entity являє собою сутність
  • Notation являє собою позначення, оголошені в DTD
NodeTypeNamed constant
1ELEMENT_NODE
2ATTRIBUTE_NODE
3TEXT_NODE
4CDATA_SECTION_NODE
5ENTITY_REFERENCE_NODE
6ENTITY_NODE
7PROCESSING_INSTRUCTION_NODE
8COMMENT_NODE
9DOCUMENT_NODE
10DOCUMENT_TYPE_NODE
11DOCUMENT_FRAGMENT_NODE
12NOTATION_NODE

Об'єкт вузла

Об'єкт вузла представлений одним вузлом в дереві. Це може бути вузол елемента, вузол атрибута, текстовий вузол або будь-який інший тип, описаний у розділі «тип вузла». Всі об'єкти можуть успадковувати властивості та методи для роботи з батьківськими та дочірніми вузлами, але не всі об'єкти мають батьківські або дочірні вузли. Наприклад, текстові вузли, які не можуть мати дочірні вузли, подібні вузли для додавання дочірніх вузлів призводять до помилки DOM.

Об'єкти в дереві DOM можуть бути адресовані та маніпулювати за допомогою методів на об'єктах. Публічний інтерфейс DOM задається в інтерфейсі прикладного програмування (API). Історія об'єктної моделі документа переплітається з історією «війн браузерів» кінця 1990-х років між Netscape Navigator та Microsoft Internet Explorer, а також з JavaScript і JScript, перші мови сценаріїв, які будуть широко впроваджені в макет системах з веб — браузерів.

Примітки
  1. tree (data structure). National Institute of Standards and Technology. Архів оригіналу за 24 листопада 2014.
  2. Teukolsky, Roselyn (2013). Barron's AP Computer Science A. Barron's. ISBN 978-1-4380-0152-4.
  3. Simply Scheme: Introducing Computer Science ch 18: Trees. College Of Engineering, University of California, Berkeley. Архів оригіналу за 22 грудня 2013.
  4. XML DOM Introduction. W3Schools. Архів оригіналу за 11 червня 2014. Процитовано 2 березня 2019.

Зовнішні посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.