Геометричне тіло
Геометри́чне ті́ло — зв'язна частина простору, обмежена замкнутою поверхнею своєї зовнішньої границі. Геометричним тілом називають також компактну множину точок і дві точки з цієї множини можна з'єднати відрізком, який цілком буде проходити в межах тіла, що вказує на склад геометричного тіла з множини внутрішніх точок.
Точка називається граничною точкою даного геометричного тіла, якщо серед як завгодно близьких до неї точок (включаючи її саму) є точки, які належать тілу, так і не належать йому. Множина всіх граничних точок тіла називається його границею. На основі цього будується уявлення геометричного тіла як частини простору, відокремленої від решти простору поверхнею — границею цього тіла. Так, наприклад, границею кулі є сфера, а границя циліндра складається з двох кругів — основ циліндра і бічної циліндричної поверхні.
Геометричне тіло за визначенням у «Началах» Евкліда (Книга XI) — частина простору, що має довжину, ширину і глибину і обмежена поверхнею.
Геометричне тіло — уявне тіло, в якому зберігаються лише форма і розміри при повному абстрагуванні від усіх інших властивостей. На відміну від реальних предметів геометричні тіла, як і всякі геометричні фігури, є уявними об'єктами.
Практичне використання
При вивченні властивостей геометричних тіл — уявних об'єктів, формуються уявлення про геометричні властивості реальних предметів (їх форму, взаємне розташування і т. д.) які можна використати в практичній діяльності.
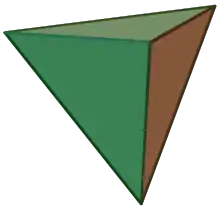
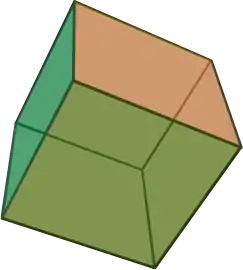
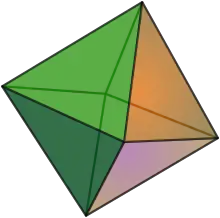
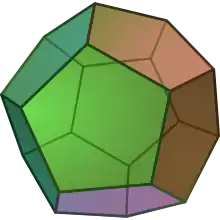
Якщо поверхня, яка обмежує тіло, складається з площин, то тіло називають багатогранником. Ці площини перетинаються по прямих, що називають ребрами. Кожна з граней є багатокутником, сторони якого є ребрами багатогранника, вершини цього багатокутника називають вершинами багатогранника. Багатогранник, у якого всі кути рівні між собою і грані рівні між собою є правильними багатокутниками, називаються правильними. Опуклих правильних багатогранників (Платонових тіл) є п'ять.
 |
 |
 |
 |
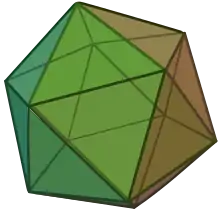 |
| Тетраедр | Гексаедр | Октаедр | Додекаедр | Ікосаедр |
|---|
Див. також
Джерела
- Погорєлов О. В. Геометрія: Стереометрія: Підруч. для 10—11 кл. серед. шк.,— 6-те вид,— К.: Освіта, 2001.— 128 с. — ISBN 966-04-0334-8.
Посилання
- Тіло геометричне // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 193. — ISBN 978-966-7407-83-4.

