Гомологія (математика)

Теорія гомологій співставляє кожному топологічному простору X послідовність абелевих груп, що є гомотопічними інваріантами простору - якщо два простори гомотопічно еквівалентні, то ці групи є ізоморфними. Це дозволяє претворити топологічну задачу на алгебраїчну, і, хоча це перетворення незворотнє, тобто при ньому втрачаються деякі геометричні властивості просторів, такий метод продемонстрував свою користь для багатьох класів задач. [1]

Загалом, гомологією топологічного простору X можна назвати ряд топологічних інваріантів Χ, виражені як класи гомології

${\displaystyle H_{0}(X),H_{1}(X),H_{2}(X),\ldots }$

де  k-та група ${\displaystyle H_{k}(X)}$ описує  k-вимірні дірки в X.[2]

Існує багато різних теорій гомологій - сімпліціарні, клітинні, гомології Чеха, Александера і Де-Рама, і, хоча вони не є еквівалентними, і приводять до різних інваріантів, в клітинних або гомотопних клітинним, просторах, тобто, таких, які можна розбити на клітини, кожна з яких гомеоморфна відкритій n-вимірній кулі, [3] усі ці теорії приводять до одних і тих же об'єктів.[4]

Першими теоріями, про які можна сказати, що вони описували гомології, були Ейлерова характеристика багатогранників і Ріманове визначення роду орієнтованої поверхні. 

Власне гомології були винайдені як спосіб аналізу і класифікації многовидів, що спирався на кількість їх циклів — замкнених петель (або, більш загально, підмноговидів), що можуть бути намальовані на деякому многовиді, але не можуть бути переведені один в інший неперервної деформацією. 

Цикли на 2-сфері

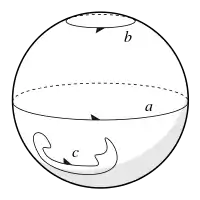
На звичайній сфері ${\displaystyle S^{2}}$, будь-який цикл можна деформацією перевести в будь-який інший, що зрозуміло з теореми Жордана, з якої слідує, що будь-яка замкнена лінія на сфері можна стягнути в точку.  Таким чином, усі цикли на сфері належать до одного класу гомологій, і всі вони гомологічні нулю. Розрізавши многовид вздовж цикла, що гомологічний нулю, розділяє його на кілька компонентів.

Цикли на торі

На відміну від сфери, на торі  можуть існувати цикли, що неможливо стягнути в точку. Цикли a, b на діаграмі вище є прикладом таких циклів. Тор можна розрізати вздовж цих циклів, і він перетвориться на фігуру, подібну до квадрата. 

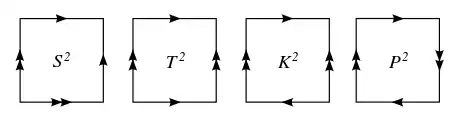
Можна сказати і навпаки, склеївши сторони квадрата у деякій послідовності, можна отримати тор. Загалом існує чотири способи попарно з'єднати сторони квадрата. Два з них дають сферу і тор, а два інших — пляшку Клейна і проективну площину. 

Чотири способи зробити закриту поверхню: потрібно склеїти сторони, що мають однакові стрілки разом.

Одновимірна сфера  ${\displaystyle S^{1}}$ (коло). Вона має один компонент з одновимірною діркою. Відповідні групи гомологій задаються як

${\displaystyle H_{k}(S^{1})={\begin{cases}\mathbb {Z} &k=0,1\\\{0\}&{\text{otherwise}}\end{cases}}}$

де ${\displaystyle \mathbb {Z} }$ — група цілих чисел, а ${\displaystyle \{0\}}$ — тривіальна група. Група ${\displaystyle H_{1}(S^{1})=\mathbb {Z} }$ представляє скінченнопороджену абелеву групу, з одним генератором, якому відповідає одновимірна дірка в колі.[5]