Автоморфізм графів

В математичному напрямку теорії графів, автоморфізм графу це форма симетрії за якої граф відображається на себе зі збереженням реберно-вершинних зв'язків.

Формально, автоморфізм графу G = (V,E) це перестановка σ множини вершин V така, що для будь-якого ребра e = (u,v), σ(e) = (σ(u),σ(v)) також ребро. Тобто, це ізоморфізм G на себе. Автоморфізм може бути визначеним таким чином і для орієнтованих, і для неорієнтованих графів. Композиція двох автоморфізмів це знов автоморфізм, і множина автоморфізмів даного графу, із операцією композиція, формує групу, групу автоморфізмів графу. В зворотному напрямку, за теоремою Фрухта, всі групи можуть бути представлені як група автоморфізмів зв'язного графу — насправді, кубічного графу.[1][2]

Обчислювальна складність

Побудова групи автоморфізмів щонайменше так само складне (в термінах теорії складності обчислень) як розв'язання проблеми ізоморфності графів. G і H ізоморфні тоді і тільки тоді, коли незв'язний граф утворений за допомогою диз'юнктивного об'єднання графів G і H має автоморфізм, що міняє місцями дві компоненти.[3]

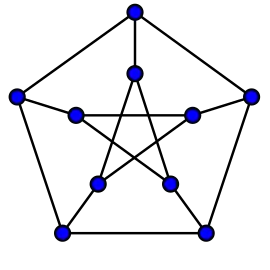
Це зображення графу Петерсена показує підгрупу його симетрій, ізоморфну до дігедральної групи D5, але граф має додаткові симетрії, які не представлені на малюнку (бо граф симетричний).

Задача автоморфізму графу полягає в визначенні чи має граф нетривіальний автоморфізм. Вона належить до класу складності NP обчислювальної складності. Подібно до проблеми ізоморфізму графів, невідомо чи існує алгоритм з поліноміальним часом чи це NP-повна задача.[4] Відомо, що задача автоморфізму графу багатозначно зводима за поліноміальний час до проблеми ізоморфізму графів, але зворотна зводимість невідома.[5][6] [7]

Зображення симетрії

Декілька дослідників візуалізації графів вивчали алгоритми зображення графів так, щоб автоморфізм графів був видимий як симетрія на малюнку. Це можна зробити через використання методу, який не був спроектованим навколо симетрій, але за можливості автоматично створює симетричні зображення,[8] або через явне визначення симетрій і використання їх як керівництва для розташування вершин в зображенні.[9] Не завжди можливо одночасно зобразити всі симетрії графу одночасно, тож виникає необхідність обирати які симетрії зображувати, а які залишати невідображеними.

Види графів за їхніми автоморфізмами

Декілька видів графів через типи їхніх автоморфізмів:

  • Асиметричний граф — неорієнтований граф без нетривіальних автоморфізмів.
  • Вершинно-транзитивний граф — неорієнтований граф в якому кожна вершина може бути відображена автоморфізмом в будь-яку іншу вершину.
  • Реберно-транзитивний граф — неорієнтований граф в якому кожне ребро може бути відображене автоморфізмом в будь-яке інше ребро.
  • Симетричний граф — такий граф, що кожна пара суміжних вершин може бути відображена в будь-яку іншу пару суміжних вершин.
  • Відстанево-транзитивний граф — такий граф, що кожна пара вершин може бути відображена автоморфізмом в будь-яку іншу пару вершин із тою самою відстанню між ними.
  • Напівсиметричний граф — реберно-транзитивний, але не вершинно-транзитивний граф.
  • Напівтранзитивний граф — вершинно-транзитивний і реберно-транзитивний, але не симетричний.
  • Кососиметричний граф — орієнтований граф з перестановкою вершин σ, яка відображає ребра на ребра, але обертає напрямок кожного з ребер. Додатково, σ має бути інволюцією.

Відношення включення між цими видами показані наступною таблицею:

Скелет додекаедра
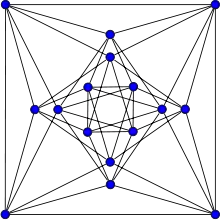граф Шріханде
граф Пейлі
відстанево-транзитивний відстанево-регулярний сильно регулярний
граф F26A
граф Науру
симетричний (дуго-транзитивний) t-транзитивний, t ≥ 2
(якщо зв'язний)
граф Хольта
граф Фолькмана
Повний дводольний граф K3,5
вершинно- та реберно-транзитивний реберно-транзитивний і регулярний реберно-транзитивний
Скелет стятого тетраедра
граф Фрухта
вершинно-транзитивний регулярний
Скелет трикутної призми
Граф Келі

Див. також

Примітки
  1. Frucht, R. (1938). Herstellung von Graphen mit vorgegebener abstrakter Gruppe.. Compositio Mathematica (German) 6: 239–250. ISSN 0010-437X. Zbl 0020.07804..
  2. Frucht, R. (1949). Graphs of degree three with a given abstract group. Canadian Journal of Mathematics 1: 365–378. ISSN 0008-414X. MR0032987..
  3. Luks, Eugene M. (1982). Isomorphism of graphs of bounded valence can be tested in polynomial time. Journal of Computer and System Sciences 25 (1): 42–65. doi:10.1016/0022-0000(82)90009-5..
  4. A. Lubiw, «Some NP-complete problems similar to Graph Isomorphism», SIAM Journal on Computing, 1O: ll-21, 1981.
  5. R. Mathon, «A note on the graph isomorphism counting problem», Information Processing Letters, 8 (1979) pp. 131—132
  6. Köbler, Johannes; Uwe Schöning, Jacobo Torán (1993). Graph Isomorphism Problem: The Structural Complexity. Birkhäuser Verlag. ISBN 0817636803. OCLC 246882287.
  7. Jacobo Torán, «the Hardness of Graph Isomorphism[недоступне посилання з червня 2019]», SIAM Journal on Computing, vol. 33, no. 5, 2004, pp. 1093—1108, DOI:10.1137/S009753970241096X
  8. Di Battista, Giuseppe; Tamassia, Roberto; Tollis, Ioannis G. (1992). Area requirement and symmetry display of planar upward drawings. Discrete and Computational Geometry 7 (1): 381–401. doi:10.1007/BF02187850.; Eades, Peter; Lin, Xuemin (2000). Spring algorithms and symmetry. Theoretical Computer Science 240 (2): 379–405. doi:10.1016/S0304-3975(99)00239-X..
  9. Hong, Seok-Hee (2002). Drawing graphs symmetrically in three dimensions. Proc. 9th Int. Symp. Graph Drawing (GD 2001). Lecture Notes in Computer Science 2265. Springer-Verlag. с. 106–108. doi:10.1007/3-540-45848-4_16..
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.