Граф F26A

Група автоморфізмів графу F26A — це група порядку 78.[3] Вона діє транзитивно на вершини, на ребра і на дуги графу. Внаслідок цього граф F26A — це симетричний граф (хоча і не відстанево-транзитивний). Згідно з переписом Фостера граф F26A — єдиний кубічний симетричний граф з 26 вершинами.[2] Він також є графом Келі для дігедральної групи D₂₆, утвореної a, ab і ab⁴, де:[4]

${\displaystyle D_{26}=\langle a,b|a^{2}=b^{13}=1,aba=b^{-1}\rangle .}$

Граф F26A є найменшим кубічним графом, в якому група автоморфізмів діє регулярно на дуги.[5]

Характеристичний поліном графу F26A дорівнює

${\displaystyle (x-3)(x+3)(x^{4}-5x^{2}+3)^{6}.\,}$

• 
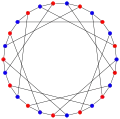  Хроматичне число графу F26A — 2.
• 
  Хроматичний індекс графу F26A — 3.
• 
  Інше зображення графу F26A.