Група Прюфера

У теорії груп p-групою Прюфера (або квазіциклічною p-групою) для фіксованого простого числа p називається єдина p-група в якій для будь-якого елементу існує рівно p коренів p-го степеня. Зазвичай позначається як Z(p^∞). Названа на честь німецького математика Гайнца Прюфера.

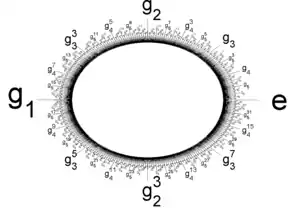
2

-група Прюфера із заданням

⟨ g n : g n +1 2 = g n, g 12 = e ⟩

, зображена як підкрупа одиничного кола на комплексній площині

Властивості

p-групу Прюфера можна розглядати як підгрупа U(1), що складається з комплексних коренів з одиниці степенів pⁿ для всіх натуральних чисел n:

\mathbb {Z} (p^{\infty })=\{\exp(2\pi im/p^{n})\mid m\in \mathbb {N} ,\,n\in \mathbb {N} \}.\;

Еквівалентно квазіциклічну p-групу можна розглядати як підгрупу Q/Z, що складається з елементів, порядок яких є степенем p:

\mathbb {Z} (p^{\infty })=\mathbb {Z} [1/p]/\mathbb {Z} .

Також p-група Прюфера може бути задана генеруючими елементами і співвідношеннями:

\mathbb {Z} (p^{\infty })=\langle \,g_{1},g_{2},g_{3},\ldots \mid g_{1}^{p}=1,g_{2}^{p}=g_{1},g_{3}^{p}=g_{2},\dots \,\rangle .

Квазіциклічна p-група є єдиною нескінченною p-групою, що є локально циклічною, тобто будь-яка скінченна підмножина її елементів породжує циклічну групу). Всі власні підгрупи квазіциклічної групи є циклічними.

Також можна записати

\mathbf {Z} (p^{\infty })=\mathbf {Q} _{p}/\mathbf {Z} _{p}

де Q_p позначає адитивну групу p-адичних чисел, а Z_p — підгрупу p-адичних цілих чисел.

Квазіциклічна група є подільною. Кожна абелева подільна група є прямою сумою копій раціональних чисел (проіндексованих деякою можливо нескінченною множиною) і копій Z(p^∞) для всіх простих чисел (зновуж проіндексованих деякими можливо нескінченними множинами). Потужності індексуючих множин для копій всіх Z(p^∞) Q визначають абелеву подільну групу із точністю до ізоморфізму.
В теорії локально компактних топологічних груп квазіциклічна p-група із дискретною топологією, є двоїстою до компактної групи p-адичних чисел.
Квазіциклічні p-групи, для всіх простих p є єдиними нескінченними групами, для яких множина підгруп є лінійно впорядкованою по вкладенню:

0\subset \mathbf {Z} /p\subset \mathbf {Z} /p^{2}\subset \mathbf {Z} /p^{3}\subset \cdots \subset \mathbf {Z} (p^{\infty }).

За цими вкладеннями p-група Прюфера є індуктивною границею своїх скінченних підгруп.
Як $\mathbb {Z}$ -модуль, p-група Прюфера є прикладом артинового але не нетерового модуля.
Кільце ендоморфізмів групи Z(p^∞) є ізоморфним кільцю p-адичних цілих чисел Z_p.

Див. також

Література

Jacobson, Nathan (2009). Basic algebra 2 (вид. 2nd). Dover. ISBN 978-0-486-47187-7.
Pierre Antoine Grillet (2007). Abstract algebra. Springer. ISBN 978-0-387-71567-4.
Kaplansky, Irving (1965). Infinite Abelian Groups. University of Michigan Press.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.