Корінь з одиниці

Корінь n-го степеня з одиниці — комплексний корінь многочлена $x^{n}-1(n\geqslant 1)$ . Іншими словами, це комплексне число $\ x$ , для якого

\ x^{n}=1.

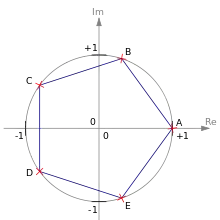
Корені п'ятого степеня з одиниці (вершини пятикутника)

Запис

Представимо одиницю в тригонометричному вигляді:

1=\cos \ 0+i\ \sin \ 0

(\cos x+i\sin x)^{n}=\cos nx+i\sin nx.\,

одержимо:

u_{k}=\cos {\frac {2\pi k}{n}}+i\ \sin {\frac {2\pi k}{n}},\quad k=0,1,...,n-1

Тут $\ u_{k}$ — корені з одиниці.

Корені з одиниці можна також записати в показниковій формі:

u_{k}=e^{\frac {2\pi ki}{n}},\quad k=0,1,...,n-1

З цих формул випливає, що кількість коренів n-го степеня з одиниці завжди рівна $n$ , і всі вони різні.

Модуль кожного кореня рівний 1. На комплексній площині корені з одиниці утворюють вершини правильного многокутника, вписаного в одиничне коло. Однією з вершин завжди є одиниця.
Якщо $\ u_{k}$ — корінь з одиниці, то спряжене до нього число ${\overline {u_{k}}}$ — теж корінь з одиниці.

Корені з одиниці — цілі алгебраїчні числа.
Корені з одиниці утворюють абелеву групу щодо операції множення. Обернений елемент для кожного елементу цієї групи рівний спряженому елементу. Зокрема, будь-який цілий степінь кореня з одиниці теж є коренем з одиниці.
Група коренів з одиниці ізоморфна адитивній групі лишків $\mathbb {Z} _{n}$ $\text{[math]}$ . Звідси випливає, що вона є циклічною групою; за породжуючий елемент групи може бути взятий довільний елемент $u_{k}$ $\text{[math]}$ , індекс $k$ $\text{[math]}$ якого взаємно простий $n$ $\text{[math]}$ .
- Наслідки:
- елемент $u_{1}$ завжди є первісним;
- якщо $n$ — просте число, то степені будь-якого кореня, окрім $\pm 1$ , охоплюють всю групу;
- число первісних коренів рівне $\varphi (n)$ , де $\varphi$ — функція Ейлера.
Якщо $n>1$ , то для суми степенів будь-якого первісного кореня з одиниці $u$ має місце формула:

\sum _{k=0}^{n-1}u^{k}={\frac {u^{n}-1}{u-1}}=0.

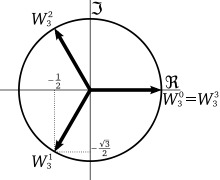
Кубічні корені з одиниці

Кубічні корені з одиниці:

\left\{1;\ {\frac {-1+i{\sqrt {3}}}{2}};\ {\frac {-1-i{\sqrt {3}}}{2}}\right\}

Корені 4-го степеня з одиниці:

\left\{1;\ +i;\ -1;\ -i\right\}

Для коренів 5-го степеня є 4 первісні елементи:

\left\{e^{2\pi ik \over 5}|k\in \{1,2,3,4\}\right\}=\left\{\left.{\frac {u{\sqrt {5}}-1}{4}}+v{\sqrt {\frac {5+u{\sqrt {5}}}{8}}}i\right|u,v\in \{-1,1\}\right\}.

Для коренів 6-го степеня первісних елементів тільки два:

\left\{{\frac {1+i{\sqrt {3}}}{2}},{\frac {1-i{\sqrt {3}}}{2}}\right\}.

Ван дер Варден Б. Л. Алгебра. — Москва : Наука, 1975. — 623 с. — ISBN 5-8114-0552-9.(рос.)
Milne, James S. (1998). Algebraic Number Theory. Course Notes. Архів оригіналу за 27 серпня 2010. Процитовано 12 серпня 2010.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.