Група бордюру
Група бордюру — це математичне поняття, що використовується для класифікації за симетріями візерунків на двовимірних поверхнях, які повторюються в одному напрямку. Такі візерунки зустрічаються часто в архітектурі і декоративному мистецтві. Математичне вивчення таких візерунків показує, що існує рівно сім типів симетрії.

Групи бордюру є двовимірними групами лінійного зсуву, які мають повторення лише в одному напрямку. Вони пов'язані зі складнішими групами орнаменту, які класифікують візерунки, що повторюються у двох напрямках, і кристалографічними групами, які класифікують візерунки, що повторюються в трьох напрямках.
Загальний опис
|
Формально, група бордюру — це клас нескінченних дискретних груп симетрії візерунків на стрічці (нескінченно широкому прямокутнику), а отже, це клас груп рухів на площині або стрічці. Група симетрії групи бордюру обов'язково містить паралельні перенесення і може містити ковзні симетрії, відбиття вздовж осі стрічки, відбиття поперек осі стрічки і обертання на . Існує сім груп бордюру, їх показано нижче в таблиці. Багато авторів перераховують групи бордюру в іншому порядку[1][2].
Фактичні групи симетрії всередині групи бордюру характеризуються найменшою відстанню паралельного перенесення і, для груп бордюру з вертикальною симетрією або поворотом на (групи 2, 5, 6 і 7), місцем розташування осі симетрії або центру повороту. У разі груп симетрії на площині додатковими параметрами є напрям вектора перенесення і, для груп бордюру з горизонтальною віссю симетрії, ковзна симетрія, або поворот на (групи 3-7), положення осі відбиття або центру обертання. Таким чином, є два ступені вільності для групи 1, три для груп 2, 3, 4 і чотири для груп 5, 6 і 7.
Для двох із семи груп бордюру (групи 1 і 4) групи симетрії породжуються одним елементом, для чотирьох груп (групи 2, 3, 5 і 6) вони породжуються двома генераторами, а для групи 7 групи симетрії вимагають трьох генераторів. Група симетрії в групах бордюрів 1, 2, 3 чи 5 є підгрупою групи симетрії останньої групи бордюру з тією самою відстанню паралельного перенесення. Група симетрії в групах бордюру 4 і 6 є підгрупою групи симетрії останньої групи бордюру з половинною відстанню паралельного перенесення. Остання група бордюру містить групу симетрії найпростішого періодичного візерунка на смузі (або площині) — послідовності точок. Будь-яке перетворення площини, що залишає недоторканим цей візерунок, можна розкласти на паралельне перенесення (x,y) → (n+x,y) і, можливо, відбиття відносно горизонтальної осі (x,y) → (x,−y) або вертикальної осі (x,y) → (−x,y) у припущенні, що осі обрано посередині двох сусідніх точок, або повороту на кут , (x,y) → (−x,−y). Таким чином, ця група бордюру містить «найбільшу» групу симетрії, яка складається з усіх цих перетворень.
Вимога дискретності вводиться для виключення групи, що містить усі паралельні перенесення, і груп, що містять довільно малі паралельні перенесення (наприклад, групи горизонтального перенесення на будь-яку раціональну відстань).
Вимога нескінченності вводиться для виключення груп, що не мають паралельного перенесення:
- група тільки з тотожним рухом (ізоморфна C1, тривіальна група порядку 1);
- група, що складається з тотожного руху і відбиття відносно горизонтальної осі (ізоморфна C2, циклічна група порядку 2);
- групи, що складаються з тотожного руху і відбиття відносно вертикальної осі;
- групи, що складаються з тотожного руху і повороту на навколо точки, розташованої на горизонтальній осі;
- групи, що складаються з тотожного руху і відбиття відносно вертикальної осі, відбиття відносно горизонтальної осі і повороту на навколо точки перетину цих осей (ізоморфна 4-групі Клейна).
Опис семи груп бордюру
Існує сім різних підгруп (з точністю до масштабу) в групі дискретних бордюрів, що генеруються паралельним перенесенням, відбиттям (уздовж осі бордюру) і поворотом на . Кожна з цих підгруп є групою симетрії бордюру і прості бордюри показано на рис. 1. Сім різних груп відповідають сімом нескінченним серіям груп осьової симетрії тривимірного простору, з [3].
Групи бордюру позначаються з використанням нотації Германа — Могена, міжнародної кристалографічної нотації[4], орбіфолдної нотації, нотації Коксетера і за допомогою символів Шенфліса:
| IUC | Кок- сетер |
Шён- фліс* Група |
Діаграма§ Орбіфолд |
Приклади позначення Конвея[5] |
Опис |
|---|---|---|---|---|---|
| p1 | [∞]+ | C∞ Z∞ |
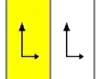 ∞∞ | F F F F F F F F hop (стрибати на одній нозі) |
(T) Тільки паралельне перенесення.
Цю групу створює один генератор, переносячи на найменшу відстань для даного періодичного візерунка. |
| p11g | [∞+,2+] | S∞ Z∞ |
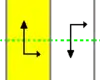 ∞× | FℲ FℲ FℲ FℲ FℲ step (крок) |
(TG) Ковзна симетрія і перенесення.
Ця група створюється одним генератором (ковзною симетрією), паралельне перенесення виходить як результат двох ковзних симетрій. |
| p1m1 | [∞] | C∞v Dih∞ |
 *∞∞ | Λ Λ Λ Λ Λ Λ Λ Λ sidle (йти боком) |
(TV) Відбиття відносно вертикальної осі і перенесення.
Група та сама, що й нетривіальна група одновимірного випадку. Група будується за допомогою паралельного перенесення і відбиття відносно вертикальної осі. |
| p2 | [∞,2]+ | D∞ Dih∞ |
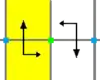 22∞ | S S S S S S S S spinning hop (стрибки з поворотом) |
(TR) Перенесення і поворот на : Група створюється двома генераторами — перенесенням і поворотом на . |
| p2mg | [∞,2+] | D∞d Dih∞ |
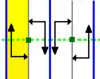 2*∞ | V Λ V Λ V Λ V Λ spinning sidle (стрибки боком з поворотом) |
(TRVG) Відбиття відносно вертикальної осі, ковзна симетрія, перенесення і поворот на : Паралельне перенесення тут виходить як результат двох ковзних симетрій, так що група генерується ковзною симетрією і або обертанням, або вертикальною симетрією. |
| p11m | [∞+,2] | C∞h Z∞×Dih1 |
 ∞* | B B B B B B B B jump (стрибок) |
(THG) Перенесення, відбиття відносно горизонтальної осі, ковзна симетрія.
Ця група генерується перенесенням і відбиттям відносно горизонтальної осі. Ковзна симетрія виходить як перенесення + відбиття. |
| p2mm | [∞,2] | D∞h Dih∞×Dih1 |
 *22∞ | H H H H H H H H spinning jump (стрибок з поворотом) |
(TRHVG) Відбиття відносно вертикальної і горизонтальної осей, паралельне перенесення і поворот на : Для цієї групи потрібні три генератори. Один з генерувальних наборів складається з перенесення і відбиттів відносно обох осей. |
- *Нотацію Шенфліса для точкової групи тут розширено для випадку нескінченного набору еквівалентних діедральних точкових симетрій
- §Діаграма показує одну фундаментальну область, виділену жовтим кольором. Осі відбиття показано синім кольором, осі ковзної симетрії — зеленим пунктиром, а точки обертання — зеленими квадратиками.
Як ми бачимо, з точністю до ізоморфізму, існує чотири групи: дві абелеві, і дві неабелеві.
Типи ґраток: похила і прямокутна
Групи можна класифікувати за типом їхньої двовимірної ґратки[6]. Похила ґратка означає, що другий напрямок не обов'язково ортогональний до напрямку повторення.
| Тип ґратки | Групи |
|---|---|
| Похилі | p1, p2 |
| Прямокутні | p1m1, p11m, p11g, p2mm, p2mg |
Вебдемонстрації та програмне забезпечення
Існують програмні графічні інструменти, що створюють двовимірні візерунки за допомогою груп бордюру. Зазвичай весь візерунок оновлюється автоматично під час редагування тексту.
- Kali — вільний застосунок для шпалер, бордюрів та інших візерунків.
- Kali для Windows і Mac Classic.
- Tess — програма (nagware) для роботи з замощеннями для різних платформ, що підтримує шпалери, бордюри, а також мозаїк Хееша.
- FriezingWorkz — вільно поширюваний стек (застосунок для Hypercard) для платформи Classic Mac, підтримує групи бордюру.
Примітки
- Coxeter, 1969, с. 47–49.
- Cederberg, 2001, с. 117–118, 165–171.
- Fisher, Mellor, 2007.
- Radaelli.
- Frieze Patterns Конвей дав нахви за характером слідів.
- Hitzer, Ichikawa, 2008.
Література
- Coxeter H. S. M. Introduction to Geometry. — New York : John Wiley & Sons, 1969. — С. 47–49. — ISBN 0-471-50458-0.
- Judith N. Cederberg. A Course in Modern Geometries, 2nd ed. — New York : Springer-Verlag, 2001. — С. 117–118, 165–171. — ISBN 0-387-98972-2.
- Fisher G.L., Mellor B. Three-dimensional finite point groups and the symmetry of beaded beads // Journal for Mathematics and the Arts. — 2007. — 21 лютого.
- Paolo G. Radaelli. Fundamentals of Crystallographic Symmetry.
- Hitzer E.S.M., Ichikawa D. Representation of crystallographic subperiodic groups by geometric algebra // Electronic Proc. of AGACSE. — Leipzig, Germany, 2008. — Вип. 3, 17–19 Aug. 2008 (21 лютого).