Дерево Калкіна — Вілфа
Дерево Калкіна — Вілфа (англ. Calkin—Wilf tree) — орієнтоване двійкове дерево, у вершинах якого розташовані додатні раціональні дроби за таким правилом:
- корінь дерева — дріб ;
- вершина з дробом має двох нащадків: (лівий) і (правий).
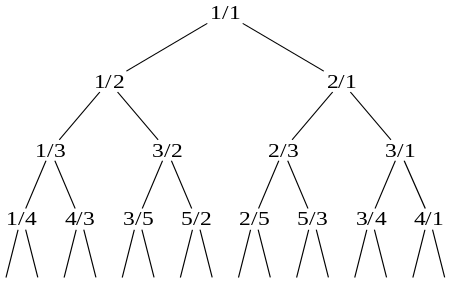
Дерево описали Нейл Калкін і Герберт С. Вілф (2000[1]) у зв'язку із задачею явного перерахунку[2] множини раціональних чисел.
Властивості дерева Калкіна — Вілфа
Основні властивості
- Всі дроби, розташовані у вершинах дерева, нескоротні;
- Будь-який нескортний раціональний дріб зустрічається в дереві рівно один раз.
Послідовність Калкіна — Вілфа
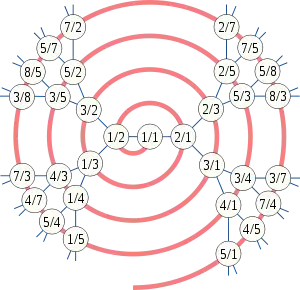
З наведених вище властивостей випливає, що послідовність додатних раціональних чисел, одержувана внаслідок обходу «в ширину»[3] (англ. breadth-first traversal) дерева Калкіна — Вілфа (звана також послідовністю Калкіна — Вілфа; див. ілюстрацію),
визначає взаємно однозначну відповідність між множиною натуральних чисел і множиною додатних раціональних чисел.
Цю послідовність можна задати рекурентним співвідношенням[4]
де і позначають відповідно цілу і дробову частини числа .
У послідовності Калкіна — Вілфа знаменник кожного дробу дорівнює чисельнику наступного.
Функція fusc
1976 року Е. Дейкстра визначив на множині натуральних чисел цілочислову функцію fusc(n) такими рекурентними співвідношеннями[5]:
- ;
- ;
- .
Послідовність значень збігається з послідовністю чисельників дробів у послідовності Калкіна-Вілфа, тобто послідовністю
- 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4, …
Таким чином (оскільки знаменник кожного дробу в послідовності Калкіна — Вілфа дорівнює чисельнику наступного), -й член послідовності Калкіна — Вілфа дорівнює , а відповідність
є взаємно однозначною відповідністю між множиною натуральних чисел і множиною додатних раціональних чисел.
Функцію може бути, крім зазначених вище рекурентних співвідношень, визначити так.
- Значення дорівнює кількості гіпердвійкових (англ. hyperbinary) подань числа , тобто подань у вигляді суми невід'ємних степенів двійки, де кожен степінь зустрічається не більше двох разів[6]. Наприклад, число 6 подається трьома такими способами:
- 6 = 4 + 2 = 4 + 1 + 1 = 2 + 2 + 1 + 1, тому .
- Значення дорівнює числу всіх непарних біноміальних коефіцієнтів вигляду , де [7].
В оригінальній статті Калкіна і Вілфа функція не згадується, але розглядається цілочисельна функція , визначена для , що дорівнює кількості гіпердвійкових подань числа , і доводиться, що відповідність
є взаємно однозначною відповідністю між множиною невід'ємних цілих чисел і множиною раціональних чисел. Таким чином, для мають місце співвідношення
Дерево Кеплера і Saltus Gerberti

Див. також
Примітки
- Див. статтю Calkin, Wilf (2000) у списку літератури.
- Тобто явного задання взаємно однозначної відповідності між множиною натуральних чисел і множиною (додатних) раціональних чисел. Стандартні доведення зліченності множини раціональних чисел зазвичай не використовують явного задання зазначеної відповідності.
- У цьому випадку обхід «у ширину» відповідає послідовному обходу кожного рівня (починаючи від верхнього) дерева Калкіна — Вілфа зліва направо (див. першу ілюстрацію).
- Знайшов Моше Ньюмен (Moshe Newman); див. книгу Айгнера і Ціглера в списку літератури, с. 108.
- Документ EWD 570: An exercise for Dr. R. M. Burstall; відтворений у книзі Dijkstra (1982) (див. список літератури), с. 215—216.
- При цьому вважають, що число 0 має єдине («порожнє») гіпердвійкове подання 0 = 0, тому .
- Див. Carlitz, L. A problem in partitions related to the Stirling numbers // Bulletin of the American Mathematical Society. — 1964. — Т. 70, № 2 (5 грудня). — С. 275—278. В цій статті визначається функція , яка виявляється пов'язаною із функцією fusc співвідношенням .
Література
- Calkin, N., Wilf H. S. Recounting the Rationals // The American Mathematical Monthly. — 2000. — Т. 107, № 4 (5 грудня). — С. 360—363. (JSTOR 2589182)
- Айгнер М., Циглер Г. Доказательства из Книги. Лучшие доказательства со времён Евклида до наших дней (пер. с англ.). — М. : Мир, 2006. — С. 105—109. — ISBN 5-03-003690-3.
- Dijkstra, E. W. Selected Writings on Computing: A Personal Perspective. — Springer-Verlag, 1982. — ISBN 0-387-90652-5. (Див. документи EWD 570 і EWD 578, відтворені в цій книзі.)
- Stern M. Über eine zahlentheoretische Funktion // Journal für die reine und angewandte Mathematik. — 1858. — Т. 55 (5 грудня). — С. 193—220.
- Щетников А. И. Алгоритм разворачивания всех числовых отношений из отношения равенства и идеальные числа Платона // ΣΧΟΛΗ. — 2008. — Т. 2 (5 грудня). — С. 55—74. — ISSN 1995-4328.