Дерево Штерна — Броко

Дерево Штерна — Броко — спосіб розташування всіх невід'ємних нескоротних дробів у вершинах упорядкованого нескінченного двійкового дерева.

У кожному вузлі дерева Штерна — Броко (іноді також званого деревом Фарея) стоїть медіанта ${\frac {m+m'}{n+n'}}$ дробів ${\frac {m}{n}}$ і ${\frac {m'}{n'}}$ , які стоять у найближчих до цього вузла лівому і правому верхніх вузлах. Початковий шматок дерева Штерна — Броко в цьому випадку має такий вигляд:

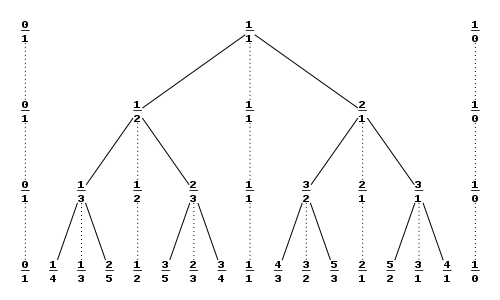
Близьким за побудовою до дерева Штерна — Броко є дерево Калкіна — Вілфа, в якому дріб ${\frac {1}{1}}$ є коренем, а всі інші вузли заповнюються за таким алгоритмом: кожна вершина ${\frac {m}{n}}$ має двох нащадків: лівого ${\frac {m}{m+n}}$ і правого ${\frac {m+n}{n}}$ .

Історія

У книзі Р. Грема, Д. Кнута, О. Паташника «Конкретна математика» відкриття «дерева Штерна — Броко» пов'язується з іменами Моріца Штерна (1858) і Ахілла Броко (1860). Однак аналогічна побудова у формі «дерева Калкіна — Вілфа» була відомою ще давньогрецьким математикам. Його описана під назвою «породження всіх відношень з відношення рівності як з матері і кореня» в двох математичних оглядах II століття, що належать Нікомаху Гераському і Теону Смірнському. Теон повідомляє, що ця конструкція була відома Ератосфену Киренському — знаменитому вченому, що жив у III столітті до н. е.

Властивості

Всі дроби в деревах Калкіна — Вілфа і Штерна — Броко нескоротні;
Кожен нескоротний дріб з'являється в дереві рівно один раз.

Для дерева Калкіна — Вілфа ці властивості легко довести, якщо зауважити, що кожному кроку деревом у напрямку до кореня відповідає елементарний крок віднімання меншого числа з більшого в алгоритмі Евкліда для пошуку найбільшого спільного дільника.

Для дерева Штерна — Броко доведення ґрунтується на такій лемі: якщо $p_{1}/q_{1}<p_{2}/q_{2}$ — дроби в двох сусідніх вузлах дерева, то $q_{1}p_{2}-q_{2}p_{1}=1$ .

Система числення Штерна — Броко

Можна скористатися символами L і R для ідентифікації лівої і правої гілки при просуванні вниз по дереву від кореня, дробу 1/1, до деякого певного дробу. Тоді кожен додатний дріб отримує єдине подання у вигляді рядка, що складається зі символів «R» і «L» (дробу 1/1 відповідає порожній рядок). Таке подання додатних раціональних чисел назвемо системою числення Штерна — Броко. Наприклад, позначення LRRL відповідає дробу 5/7.

Див. також

Література

Айгнер М., Циглер Г. Доказательства из Книги. Лучшие доказательства со времён Евклида до наших дней. — М. : Мир, 2006. — С. 105—109. — ISBN 5-03-003690-3..
Грэхем Р., Кнут Д., Паташник О. Конкретная математика. Основание информатики. — М. : Мир, 1998. — 704 с. — ISBN 5-03-001793-3..
Щетников А. И. Алгоритм разворачивания всех числовых отношений из отношения равенства и идеальные числа Платона // ΣΧΟΛΗ. — 2008. — Т. 2 (3 листопада). — С. 55—74. — ISSN 1995-4328.
Brocot A. Calcul des rouages par approximation, nouvelle méthode // Revue Chonométrique. — 1861. — Т. 3 (3 листопада). — С. 186—194.
Stern M. Über eine zahlentheoretische Funktion // Journal für die reine und angewandte Mathematik. — 1858. — Т. 55 (3 листопада). — С. 193—220.

Посилання

The Stern — Brocot or Farey Tree(англ.)
Кноп К. Недвоичная система // Домашний компьютер. — 2001. — № 8 (3 листопада). Архівовано з джерела 12 березня 2007.
Онлайн-демонстратор наближення раціональних чисел за допомогою дерева Штерна — Броко

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.