Дистанційно-регулярний граф

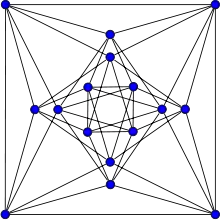
Визначення дистанційно-регулярного графа[1][2]:

Дистанційно-регулярний граф — це неорієнтований, зв'язний, обмежений, регулярний граф ${\displaystyle \Gamma =(V,E)}$ діаметром ${\displaystyle D}$, для якого справедливо, що існують числа

${\displaystyle b_{0}=k\quad b_{1},\,\dots \,,\,b_{D-1}\,\quad c_{1}=1,\quad c_{2},\,\dots ,\,c_{D}}$

такі, що для кожної пари вершин ${\displaystyle (u,v)}$, відстань між якими ${\displaystyle d(u,v)=j}$ справедливо:

(1) число вершин, інцидентних ${\displaystyle u}$, розташованих на відстані ${\displaystyle j-1}$ від ${\displaystyle v}$ є ${\displaystyle c_{j}}$ (${\displaystyle 1\leqslant j\leqslant D}$): (2) число вершин, інцидентних ${\displaystyle u}$, розташованих на відстані ${\displaystyle j+1}$ від ${\displaystyle v}$ є ${\displaystyle b_{j}}$ (${\displaystyle 0\leqslant j\leqslant D-1}$).

Масив ${\displaystyle \left\{k,\,b_{1},\,\dots ,\,b_{D-1}\,;1,\,c_{2},\,\dots ,\,c_{D}\right\}}$ є масив перетинів дистанційно-регулярного графа, де ${\displaystyle k}$ — валентність графа.

Дистанційно-регулярний граф з діаметром 2 є сильно регулярним[1] і обернене твердження теж істинне (за умови, що граф є зв'язним).

На перший погляд дистанційно-транзитивний граф і дистанційно-регулярний граф є дуже близькими поняттями. Дійсно, кожен дистанційно-транзитивний граф є дистанційно-регулярним. Однак їх природа різна. Якщо дистанційно-транзитивний граф визначається виходячи з симетрії графа через умову автоморфізму, то дистанційно-регулярний граф визначається з умови його комбінаторної регулярності[1].

Автоморфізм дистанційно-транзитивного графа викликає його регулярність, і відповідно, наявність чисел перетинів ${\displaystyle a_{j},\,b_{j},\,c_{j}}$. Однак, якщо існує комбінаторна регулярність, і визначені числа перетинів для графа, і він дистанційно-регулярний, то автоморфізм з цього не випливає.

Якщо з дистанційно-транзитивності графа випливає його дистанційно-регулярність, то зворотне не істинне.

Це доведено 1969 року, ще до введення в ужиток терміна дистанційно-транзитивний граф, групою радянських математиків[3] (Адельсон-Вельський Г. М., Вейсфейлер Б. Ю., Леман А. А., Фараджев І. А.). Найменший дистанційно-регулярний граф, який не є дистанційно-транзитивним — це граф Шрікханде. Єдиний тривалентний граф цього типу — це 12-клітка Татта, граф зі 126 вершинами.

нехай ${\displaystyle \Gamma =(V,E)}$ — транзитивно-регулярний граф діаметра ${\displaystyle D}$ і порядку ${\displaystyle n}$, а ${\displaystyle u}$ і ${\displaystyle v}$ — пара вершин, віддалених одна від одної на відстань ${\displaystyle d=(u,v)}$. Тоді множину вершин, інцидентних до ${\displaystyle u}$ можна розбити на три множини ${\displaystyle A}$, ${\displaystyle B}$ і ${\displaystyle C}$, залежно від їх відстані ${\displaystyle d(v,w)}$ до вершини ${\displaystyle v}$, де вершина ${\displaystyle w}$ інцидентна до ${\displaystyle u}$:

${\displaystyle \left\{w\in A\,:d(v,w)=j\right\},\quad \left\{w\in B\,:d(v,w)=j+1\right\},\quad \left\{w\in C\,:d(v,w)=j-1\right\}}$ .

кардинальні числа ${\displaystyle |A|,\,|B|,\,|C|}$ цих множин ${\displaystyle a_{j}=|A|,\,b_{j}=|B|,\,c_{j}=|C|}$ є числами перетинів, а масив перетинів є

${\displaystyle \iota (\Gamma )={\begin{Bmatrix}\ast &c_{1}&c_{2}&\dots &c_{D-1}&c_{D}\\a_{0}&a_{1}&a_{2}&\dots &a_{D-1}&a_{D}\\b_{0}&b_{1}&b_{2}&\dots &b_{D-1}&\ast \\\end{Bmatrix}}}$

якщо ${\displaystyle k}$ — валентність графа, то ${\displaystyle b_{0}=k}$, ${\displaystyle c_{0}=0}$ а ${\displaystyle c_{1}=1}$. Більш того, ${\displaystyle a_{i}+b_{i}+c_{i}=k}$ . Тому масив перетинів записується як:

${\displaystyle \iota (\Gamma )={\begin{Bmatrix}k,\,b_{1},\,\dots ,\,b_{D-1}\,;\,1,\,c_{2},\,\dots ,\,c_{D}\end{Bmatrix}}}$

Нехай граф ${\displaystyle \Gamma (V,E)}$ — транзитивно-регулярний діаметра ${\displaystyle D}$, ${\displaystyle n=|V|}$ — кардинальне число його множини вершин ${\displaystyle V}$, а ${\displaystyle k}$ — валентність графа. Визначимо[1] множину матриць відстаней (англ. distance matrices) розміру ${\displaystyle n\times n}$${\displaystyle \left\{\mathbf {A} _{0},\,\mathbf {A} _{1},\,\dots ,\,\mathbf {A} _{D}\right\}}$ як:

${\displaystyle \left(\mathbf {A} _{h}\right)_{r,s}={\begin{cases}1&:\,d(v_{r},v_{s})=h,\\0&:\,d(v_{r},v_{s})\neq h\end{cases}}}$

Нехай на транзитивно-регулярному графі ${\displaystyle \Gamma }$ діаметру ${\displaystyle D}$ задано алгебру суміжності ${\displaystyle \mathbb {A} (\Gamma )}$[6], тобто матричну підалгебру ${\displaystyle M_{n\times n}(\mathbb {R} )}$ поліномів матриці суміжності ${\displaystyle \mathbf {A} }$. Її розмірністю буде ${\displaystyle dim(\mathbb {A} )=D+1}$, а базисом — множина матриць відстаней ${\displaystyle \left\{\mathbf {A} _{0},\,\mathbf {A} _{1},\,\dots ,\,\mathbf {A} _{D}\right\}}$[7].

• Повні графи
• Циклічні графи
• Графи Мура, зокрема граф Петерсена і граф Гофмана — Синглтона
• Сильно регулярні графи
• Непарні графи

• Адельсон-Вельский Г.М., Вейсфелер Б.Ю., Леман А.А., Фараджев И.А. Об одном примере графа, не имеющнго транзитивной группы автоморфизмов // Доклады Академии наук. — 1969. — Т. 185, № 5 (3 березня). — С. 975—976.
• Biggs N.L. Algebraic Graph Theory. — 2nd. — Cambridge University Press, 1993. — 205 с.
• Brouwer A., Cohen A.M., Neumaier A. Distance Regular Graphs. — Berlin, New York : Springer-Verlag, 1989. — ISBN 3-540-50619-5, 0-387-50619-5.
• van Dam E.R., Koolen J.H., Tanaka H. Distance-regular graphs // The Electronic Journal of Combinatorics : dynamic surveys. — 2006. — No. DS22 (3 March).
• Godsil C. D. Algebraic combinatorics. — N. Y. : Chapman and Hall, 1993. — С. xvi+362. — (Chapman and Hall Mathematics Series) — ISBN 0-412-04131-6.
• Lauri J., Scapelatto R. Topics in Graph Automorphisms and Reconstruction. — 2nd. — Combridge : Combridge University Press, 2016. — 188 с.