Доцентрове прискорення

Нормальне прискорення ${\displaystyle a_{n}}$ обчислюють за формулою

${\displaystyle a_{n}={\frac {v^{2}}{R}}}$

або (з використанням співвідношення ${\displaystyle v=\omega R}$)

${\displaystyle a_{n}=\omega ^{2}R}$,

де ${\displaystyle v}$ — (миттєва) лінійна швидкість руху по траєкторії, ${\displaystyle \omega }$ — (миттєва) кутова швидкість руху відносно центра кривини траєкторії, ${\displaystyle R}$ — радіус кривини траєкторії в даній точці.

Вирази можна переписати у векторному вигляді:

${\displaystyle \mathbf {a} _{n}={\frac {v^{2}}{R}}\mathbf {n} =\omega ^{2}R\mathbf {n} }$.

Тут ${\displaystyle \mathbf {n} }$ — одиничний вектор, напрямлений від даної точки траєкторії до центра кривини траєкторії.

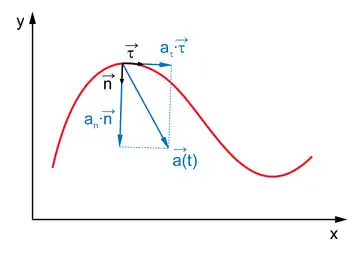
Ці формули застосовні як до часткової ситуації рівномірного руху (${\displaystyle |{\vec {v}}|=\,}$const), так і до довільного випадку. У рівномірному випадку нормальне прискорення збігається з повним. У загальному ж випадку нормальне прискорення — це лише складова вектора ${\displaystyle {\vec {a}}}$, перпендикулярна до траєкторії руху (вектора ${\displaystyle {\vec {v}}}$), а в повний вектор прискорення входить ще й тангенціальна складова ${\displaystyle a_{\tau }=dv/dt}$, співнапрямлена з дотичною до траєкторії[1].

Для розкладання прискорення на тангенціальне і нормальне можна продиференціювати за часом вектор швидкості, заданий у вигляді ${\displaystyle \mathbf {v} =v\,\mathbf {\tau } }$ через одиничний вектор дотичної ${\displaystyle \mathbf {\tau } }$:

${\displaystyle \mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d(v\mathbf {\tau } )}{dt}}={\frac {\mathrm {d} v}{\mathrm {d} t}}\,\mathbf {\tau } +v{\frac {d\mathbf {\tau } }{dt}}=\mathbf {a} _{\tau }+v{\frac {d\mathbf {\tau } }{dl}}{\frac {dl}{dt}}=\mathbf {a} _{\tau }+v^{2}{\frac {d\mathbf {\tau } }{dl}}=\mathbf {a} _{\tau }+{\frac {v^{2}}{R}}{\frac {d\mathbf {\tau } }{d\varphi }}=\mathbf {a} _{\tau }+{\frac {v^{2}}{R}}\,\mathbf {n} }$.

Тут перший доданок — тангенціальне прискорення, а другий — нормальне прискорення. Через ${\displaystyle \mathbf {n} }$ позначено одиничний вектор нормалі, ${\displaystyle R}$ — радіус кривини траєкторії в даній точці, ${\displaystyle dl}$ — елемент довжини траєкторії. Малу ділянку будь-якої кривої можна вважати дугою кола, причому її радіус і є радіусом кривини ${\displaystyle R}$. У ланцюжку перетворень використано очевидні співвідношення ${\displaystyle dl/dt=v}$ і ${\displaystyle dl=R\,d\varphi }$ (де ${\displaystyle d\varphi }$ — малий кут повороту навколо центру кривини).

Рівність ${\displaystyle d\mathbf {\tau } /d\varphi =\mathbf {n} }$ випливає з геометричних міркувань. Різниця ${\displaystyle \Delta \mathbf {\tau } =\mathbf {\tau } '-\mathbf {\tau } }$ одиничних дотичних векторів у розглянутій (${\displaystyle \mathbf {\tau } }$) і близькій до неї (${\displaystyle \mathbf {\tau } '}$) точках траєкторії становить за величиною ${\displaystyle 2\sin(\Delta \varphi /2)}$, де ${\displaystyle \Delta \varphi }$ — кут між ${\displaystyle \mathbf {\tau } '}$ і ${\displaystyle \mathbf {\tau } }$. Ця різниця напрямлена під кутом ${\displaystyle \Delta \varphi /2}$ до нормалі ${\displaystyle \mathbf {n} }$ у розглянутій точці. За малого ${\displaystyle \Delta \varphi }$ буде збіг із вектором нормалі ${\displaystyle \mathbf {n} }$. Також за малого ${\displaystyle \Delta \varphi }$ можливий розклад синуса в ряд Тейлора. В результаті прийдемо до ${\displaystyle \Delta \mathbf {\tau } =\Delta \varphi \,\mathbf {n} }$ або, для нескінченно малих, ${\displaystyle d\mathbf {\tau } /d\varphi =d\varphi /d\varphi \,\mathbf {n} }$.

Обчислення радіуса кривини і координат центра кривини траєкторії є математичною задачею (див. Кривина). Якщо криву задано рівнянням ${\displaystyle y=f(x)}$, то радіус її кривини в точці (${\displaystyle x}$, ${\displaystyle y}$) знаходять як[2]

${\displaystyle R={\frac {(1+f'^{2})^{3/2}}{|f''|}}}$,

а положення центра кривини — за формулами[2]

${\displaystyle \xi =x-{\frac {f'(1+f'^{2})}{f''}},\qquad \eta =y+{\frac {1+f'^{2}}{f''}}}$.

Одиничний вектор нормалі в такому випадку буде (${\displaystyle {\vec {i}}}$, ${\displaystyle {\vec {j}}}$ — орти)

${\displaystyle {\vec {n}}={\frac {\xi -x}{R}}\,{\vec {i}}+{\frac {\eta -y}{R}}\,{\vec {j}}}$.

Якщо відома залежність радіус-вектора матеріальної точки від часу ${\displaystyle {\vec {r}}(t)}$ (з математичної точки зору це означає задання траєкторії в параметричному вигляді), то радіус кривини можна знайти через прискорення:

${\displaystyle R={\frac {v^{2}}{\sqrt {a^{2}-a_{\tau }^{2}}}}}$,

де ${\displaystyle {\vec {a}}=d{\vec {v}}/dt}$ і ${\displaystyle a_{\tau }=dv/dt}$; попередньо знаходять швидкість як ${\displaystyle {\vec {v}}=d{\vec {r}}/dt}$. Центр кривини в загальному випадку не буде збігатися з початком відліку радіус-вектора.

Те, що розкладання вектора прискорення на компоненти — одну вздовж дотичної до траєкторії (тангенціальне прискорення) і іншу ортогональну їй (нормальне прискорення) — може бути зручним і корисним, досить очевидно. Під час руху зі сталою за модулем швидкістю тангенціальна складова стає рівною нулю, тобто в цьому важливому окремому випадку залишається тільки нормальна складова. Крім того, кожна з цих складових має яскраво виражені власні властивості і структуру, і нормальне прискорення містить в структурі своєї формули досить важливе і нетривіальне геометричне наповнення. Вкрай важливий також окремий випадок руху по колу.

Абсолютна величина тангенціального прискорення залежить тільки від шляхового прискорення, збігаючись з його абсолютною величиною, на відміну від абсолютної величини нормального прискорення, яка від шляхового прискорення не залежить, зате залежить від шляхової швидкості.

Першим правильні формули для доцентрового прискорення (або відцентрової сили) отримав, напевно, Гюйгенс. Практично з цього часу розгляд доцентрового прискорення входить у звичайну техніку розв'язування механічних задач.

Дещо пізніше ці формули зіграли істотну роль у відкритті закону всесвітнього тяжіння (формулу доцентрового прискорення використано для отримання закону залежності гравітаційної сили від відстані до джерела гравітації, виходячи з виведеного зі спостережень третього закону Кеплера).

До XIX століття розгляд доцентрового прискорення стає вже абсолютно звичним як для чистої науки, так і для інженерних застосувань.

• Тангенціальне прискорення
• Кривина
• Відцентрова сила

• https://www.eduget.com/course/fizika_podgotovka_k_zno-2325/

• Нормальне прискорення // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 134. — ISBN 978-966-7407-83-4.