Експоненційний об'єкт

Нехай в категорії ${\displaystyle C}$ існують бінарні добутки. Тоді експоненціал ${\displaystyle Z^{Y}}$ за означенням є універсальним морфізмом з функтора ${\displaystyle [-]\times Y}$ у ${\displaystyle Z}$. (Функтор ${\displaystyle [-]\times Y}$ з ${\displaystyle C}$ у ${\displaystyle C}$ відображає об'єкт ${\displaystyle X}$ в ${\displaystyle X\times Y}$ і морфізми ${\displaystyle \varphi }$ у ${\displaystyle \varphi \times \mathrm {id} _{Y}}$).

Іншими словами експоненціал ${\displaystyle Z^{Y}}$ об'єктів ${\displaystyle Z}$ і ${\displaystyle Y}$ категорії ${\displaystyle C}$ є об'єктом, разом з морфізмом ${\displaystyle eval\colon Z^{Y}\times Y\to Z}$, що називається відображенням оцінки такими, що для будь-якого об'єкта ${\displaystyle X}$ і морфізма ${\displaystyle g\colon X\times Y\to Z}$ існує єдиний морфізм ${\displaystyle \lambda g\colon X\to Z^{Y}}$, для якого діаграма нижче є комутативною:

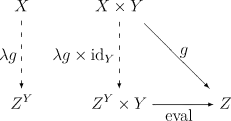
Universal property of the exponential object

Якщо експоненціал ${\displaystyle Z^{Y}}$ існує для всіх ${\displaystyle Z}$ у ${\displaystyle C}$, то функтор, що відправляє ${\displaystyle Z}$ у ${\displaystyle Z^{Y}}$ є правим спряженим до ${\displaystyle [-]\times Y}$. У цьому випадку існує натуральна бієкція:

${\displaystyle \mathrm {Hom} (X\times Y,Z)\cong \mathrm {Hom} (X,Z^{Y})}$.

• У категорії множин експоненціал ${\displaystyle Z^{Y}}$ це множина всіх функцій з ${\displaystyle Y}$ у ${\displaystyle Z}$. Для будь-якого відображення ${\displaystyle g\colon (X\times Y)\rightarrow Z}$ відображення ${\displaystyle \lambda g\colon X\to Z^{Y}}$ задається як:

${\displaystyle \lambda g(x)(y)=g(x,y)}$.

• У категорії топологічних просторів експоненціал ${\displaystyle Z^{Y}}$ існує, якщо ${\displaystyle Y}$ — локально компактний гаусдорфів простір. В цьому випадку ${\displaystyle Z^{Y}}$ - множина неперервних функцій з ${\displaystyle Y}$ у ${\displaystyle Z}$ з компактно-відкритою топологією. Якщо ${\displaystyle Y}$ не є локально компактним гаусдорфовим простором, то експоненціал може не існувати (простір ${\displaystyle Z^{Y}}$ буде існувати, але відображення ${\displaystyle \lambda }$ може не бути неперервним). З цієї причини категорія топологічних просторів не є декартово замкнутою.

• Adámek, Jiří; Horst Herrlich; George Strecker (2006) [1990]. Abstract and Concrete Categories (The Joy of Cats). John Wiley & Sons.
• Awodey, Steve (2010). Chapter 6: Exponentials. Category theory. Oxford New York: Oxford University Press. ISBN 978-0199237180.