Зрізаний додекаедр

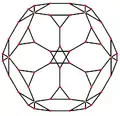
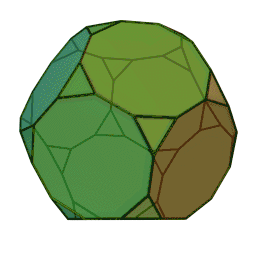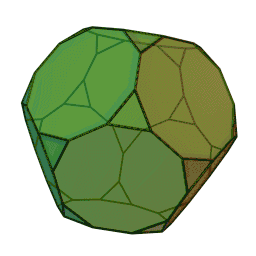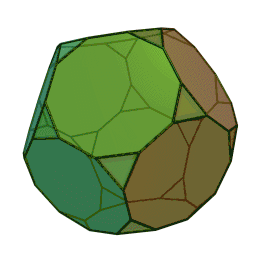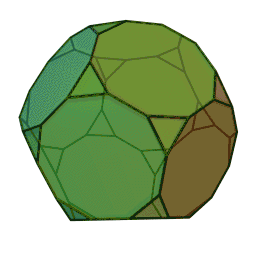
Зрі́заний додека́едр — напівправильний многогранник, відноситься до архімедових тіл, що складається із 12 правильних десятикутників і 20 правильних трикутників, 60 вершин і 90 ребер. Двоїстий до зрізаного додекаедра многогранник — триакісікосаедр.

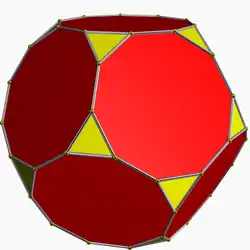
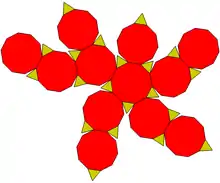
Тривимірна модель зрізаного додекаедра

Отримати даний многогранник можна за рахунок зрізання всіх вершин правильного додекаедра на третину від первісної довжини ребра, за рахунок чого п'ятикутні площини стають десятикутними, а їхні вершини перетворюються на трикутники.

Використовується в ізохорно гіперболічному заповненні простору теселяцією, об'ємами зрізаного додекаедра з дисфеноїдно вершинною фігуристикою.

Ортогональні проєкції

Формули

Знаючи довжину ребра зрізаного додекаедра — a - отримуємо:

Математичний опис
Об'єм	$V={\frac {5}{12}}\left(99+47{\sqrt {5}}\right)a^{3}\approx 85.0396646a^{3}$
Площа поверхні	$S=5\left({\sqrt {3}}+6{\sqrt {5+2{\sqrt {5}}}}\right)a^{2}\approx 100.99076a^{2}$

Прямокутна система координат

Наступні декартові координати визначають вершини зрізаного додекаедра з довжиною ребра 2(τ-1), і з центром в початку координат —

Розгортка зрізаного додекаедра

: (0, ±1/τ, ±(2+τ)): (±(2+τ), 0, ±1/τ): (±1/τ, ±(2+τ), 0): (±1/τ, ±τ, ±2τ): (±2τ, ±1/τ, ±τ): (±τ, ±2τ, ±1/τ): (±τ, ±2, ±τ²): (±τ², ±τ, ±2): (±2, ±τ², ±τ)

де τ = (1 + √5) / 2 є золотим січенням (також пишеться φ).

Графічне зображення

Сферична плитка

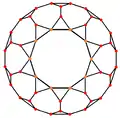
Зрізаний додекаедр можна подати у вигляді сферичної плитки, і спроєктувати на площину у вигляді стереографічної проєкції. Ця проєкція буде конформною, зберігаючи кути, але не площини чи ребра багатогранника. Прямі лінії на сфері проєктуватимуться як дуги на площині.

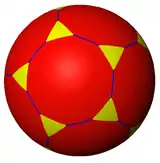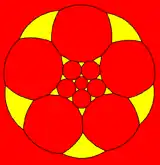Сферична плитка	Стереографічна проєкція (лицева)
	центровано десятикутником	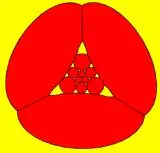центровано трикутником

Джерела

Weisstein, Eric W. Cuboctahedron(англ.) на сайті Wolfram MathWorld.
Пчелінцев В. О. Кристалографія, кристалохімія та мінералогія. Навчальний посібник для студентів вищих навчальних закладів. Суми: Вид-во СумДУ, 2008, — 232с.
Гордєєва Є. П., Величко В. Л. Нарисна геометрія. Багатогранники (правильні, напівправильні та зірчасті). Частина І. Навчальний посібник. Луцьк: Редакційно-видавничий відділ ЛДТУ, 2007, — 198с.
П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. Многоугольники и многогранники. Энциклопедия элементарной математики. Москва: Государственное издательство физико-математической литературы, 1963, — 568с.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.