Квантовий осцилятор

В класичній фізиці функція Гамільтона для лінійного (одновимірного) гармонічного осцилятора має вигляд

${\displaystyle H={\frac {p_{x}^{2}}{2\mu }}+{\frac {\mu \omega _{0}^{2}}{2}}x^{2}.}$,

де ${\displaystyle p_{x}}$- імпульс частинки, ${\displaystyle \mu }$- її маса, ${\displaystyle x}$- відхилення від положення рівноваги, а ${\displaystyle \omega _{0}}$- власна циклічна частота осцилятора.

Необхідно відзначити, що гармонічний осцилятор є до деякої міри ідеалізацією, оскільки значення потенціальної енергії ${\displaystyle U(x)={\frac {\mu \omega _{0}^{2}}{2}}x^{2}}$ означає, що по мірі віддалення від положення рівноваги сила необмежено зростає. У всіх реальних випадках, починаючи з деяких значень амплітуди, починаються помітні відхилення від гармонічності, а при дуже великих відхиленнях — сила взаємодії прямує до нуля, а ${\displaystyle U}$ — до постійної величини. Проте для невеликих амплітуд коливань цілком доречно користуватися поняттям гармонічного осцилятора.

В квантовій механіці під лінійним квантовим гармонічним осцилятором (ЛКГО) розуміють систему, яка описується оператором Гамільтона, котрий можна подати у вигляді:

${\displaystyle {\hat {H}}={\frac {{\hat {p}}_{x}^{2}}{2\mu }}+{\frac {\mu \omega _{0}^{2}}{2}}{\hat {x}}^{2}.}$,

де ${\displaystyle {{\hat {p}}_{x}}}$- оператор імпульсу, а ${\displaystyle {\hat {x}}}$- оператор координати. Відповідно до цього гамільтоніану рівняння Шредінгера в «х — представленні» для стаціонарних (основних) станів осцилятора має вигляд:

${\displaystyle -{\frac {h^{2}}{2\mu }}\cdot {\frac {d^{2}\psi }{dx^{2}}}+{\frac {\mu \omega _{0}^{2}}{2}}\cdot x^{2}\psi =E\psi }$

Для розв'язку цього рівняння можна ввести наступні безрозмірні величини:

${\displaystyle \xi ={\frac {x}{x_{0}}},}$ ${\displaystyle x_{0}={\sqrt {\frac {h}{\mu \omega _{0}}}},}$ ${\displaystyle \lambda ={\frac {2E}{h\omega _{0}}}}$

Позначаючи диференцювання по ${\displaystyle \xi }$ штрихом та розглядаючи ${\displaystyle \psi }$ як функцію ${\displaystyle \xi }$, після елементарних перетворень приводимо рівняння Шредінгера до канонічного вигляду:

${\displaystyle \xi ''+(\lambda -\xi ^{2})\psi =0.}$

Нам необхідно знайти скінченні, неперервні та однозначні розв'язки цього рівняння в інтервалі ${\displaystyle -\propto \;<\xi <+\propto \;}$. Такі розв'язки мають місце не при всіх значеннях параметра ${\displaystyle \lambda }$, а лише при: ${\displaystyle \lambda =2n+1,~n=0,1,2,3,...,}$, при чому відповідні власні функції ${\displaystyle \psi _{n}(\xi )}$ дорівнюють

${\displaystyle \psi _{n}(\xi )=e^{-{\frac {\xi ^{2}}{2}}}H_{n}(\xi ),~~H_{n}(\xi )={\frac {(-1)^{n}}{\sqrt {2^{n}n!{\sqrt {\pi }}}}}e^{\xi ^{2}}{\frac {d^{n}e^{-\xi ^{2}}}{d\xi ^{n}}}}$.

Тут ${\displaystyle H_{n}(\xi )}$ — нормовані поліноми Ерміта ${\displaystyle n}$- го порядку. При цьому, множник перед ${\displaystyle e^{\xi ^{2}}}$ вибраний так, що функція ${\displaystyle \psi _{n}(\xi )}$ є нормована по ${\displaystyle \xi }$ до 1:

${\displaystyle \int _{-\propto \;}^{\propto \;}\psi _{n}^{2}(\xi )\,d\xi =\int _{-\propto \;}^{\propto \;}e^{-\xi ^{2}}H_{n}^{2}(\xi )\,d\xi =1}$.

Таким чином, одної вимоги неперервності та скінченності ${\displaystyle \psi }$ виявляється достатньо, щоб параметр ${\displaystyle \lambda }$ набував лише дискретних значень. Проте, оскільки цей параметр визначає енергію, тому для неї будемо мати також дискретні значення ${\displaystyle E_{n}}$:

${\displaystyle E_{n}=\hbar \omega _{0}\left(n+{\frac {1}{2}}\right),n=0,1,2,3,...}$

Ця формула показує, що енергія осцилятора ${\displaystyle E}$ може приймати тільки дискретні значення. Число ${\displaystyle n}$, яке визначає номер квантового рівня, називають головним квантовим числом. Енергетичні рівні квантового осцилятора еквідистантні, тобто відстань між двома сусідніми рівнями є сталою величиною, що дорівнює ${\displaystyle \hbar \omega _{0}}$. Навіть в основному стані ${\displaystyle n=0}$ енергія осцилятора відмінна від нуля: ${\displaystyle E_{0}=\hbar \omega _{0}/2}$. Нарешті можна записати власну функцію, яка відповідає ${\displaystyle n}$- му значенню енергії в «${\displaystyle x}$»- представленні у вигляді:

${\displaystyle \psi _{n}(x)={\frac {1}{\sqrt {x_{0}}}}e^{-{\frac {x^{2}}{x_{0}^{2}}}}H_{n}(x/x_{0}).}$

Ці функції нормовані так, що ${\displaystyle \int _{-\propto \;}^{\propto \;}\psi _{n}^{2}(x)\,dx=1}$. Користуючись наведеними вище формулами можна виписати декілька власних функцій у явному вигляді:

${\displaystyle \psi _{0}(x)={\frac {1}{\sqrt {x_{0}{\sqrt {\pi }}}}}e^{-{\frac {x^{2}}{2x_{0}^{2}}}},~~\psi _{1}(x)={\frac {1}{\sqrt {2x_{0}{\sqrt {\pi }}}}}e^{-{\frac {x^{2}}{2x_{0}^{2}}}}\cdot {\frac {2x}{x_{0}}},~~\psi _{2}(x)={\frac {1}{\sqrt {2^{3}x_{0}{\sqrt {\pi }}}}}e^{-{\frac {x^{2}}{2x_{0}^{2}}}}\left(4{\frac {x^{2}}{x_{0}^{2}}}-2\right).}$

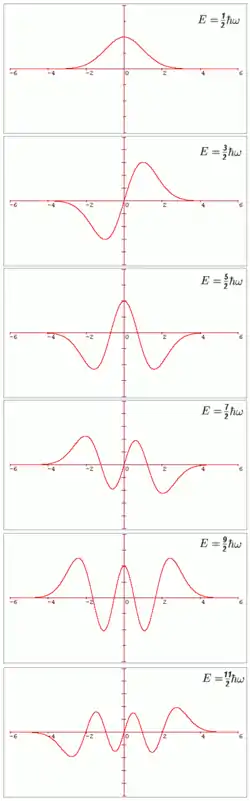
Перша функція не дорівнює нулю у всій області визначення, за виключенням граничних випадків ${\displaystyle x=\pm \;\propto \;}$. Друга функція дорівнює нулю при ${\displaystyle x=0}$. Точку, де хвильова функція дорівнює нулю, можна назвати вузлом. Третя функція дорівнює нулю при ${\displaystyle x=\pm \;{\frac {x_{0}}{\sqrt {2}}}}$ і має таким чином, два вузли. Тут можна відмітити, що кількість вузлів хвильової функції дорівнює її номеру ${\displaystyle n}$. Ця властивість справедлива для будь-якого значення ${\displaystyle n}$. Таким чином, квантове число дорівнює числу вузлів власної функції. Ці функції зображені на верхньому малюнку. Вигляд функцій ${\displaystyle \psi _{n}}$ аналогічний вигляду функції ${\displaystyle U_{n}(x)}$, який показує коливання закріпленої на кінцях струни.

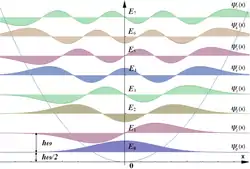
Щоб отримати ще повніше уявлення про квантові стани осцилятора, можна привести нижній малюнок для потенціальної функції осцилятора

${\displaystyle U(x)={\frac {\mu \omega _{0}^{2}}{2}}x^{2}}$.

Вздовж осі ординат відкладено потенційна енергія, а вздовж осі абсцис — відхилення ${\displaystyle x}$.

Якщо визначити оператори народження ${\displaystyle {\hat {a}}^{+}}$ та знищення ${\displaystyle {\hat {a}}}$ як

${\displaystyle {\hat {a}}^{+}={\frac {1}{\sqrt {2\hbar \omega }}}(\omega q-i{\hat {p}})~,~~~{\hat {a}}={\frac {1}{\sqrt {2\hbar \omega }}}(\omega q+i{\hat {p}})}$,

то гамільтоніан квантового осцилятора можна записати так:

${\displaystyle {\hat {H}}=\hbar \omega \left({\hat {a}}^{+}{\hat {a}}+{\frac {1}{2}}\right)}$.

Оператори народження та знищення задовольняють комутаційному співвідношенню:

${\displaystyle {\hat {a}}{\hat {a}}^{+}-{\hat {a}}^{+}{\hat {a}}=1}$.

Власні функції гармонічного осцилятора тоді мають вигляд

${\displaystyle \psi _{n}={\sqrt {n!}}({\hat {a}}^{+})^{n}\psi _{0}}$,

або, використовуючи нотацію кет і бра-векторів:

${\displaystyle |n>={\sqrt {n!}}({\hat {a}}^{+})^{n}|0\rangle }$.

Загалом дія оператора народження на гармонійний оператор у стані ${\displaystyle |n\rangle }$ призводить до переходу в стан ${\displaystyle |n+1\rangle }$:

${\displaystyle {\hat {a}}^{+}|n\rangle ={\sqrt {n+1}}|n+1\rangle }$.

Дія оператора знищення на стан |n> призводить до переходу в стан |n-1>:

${\displaystyle {\hat {a}}|n\rangle ={\sqrt {n}}|n-1\rangle }$

Оператор

${\displaystyle {\hat {N}}={\hat {a}}^{+}{\hat {a}}}$

називають оператором числа частинок, оскільки для нього справедливе співвідношення.

${\displaystyle {\hat {N}}|n\rangle =n|n\rangle }$

• Федорченко А. М. Квантова механіка, термодинаміка і статистична фізика // Теоретична фізика. — К. : Вища школа, 1993. — Т. 2. — 415 с.
• Юхновський І. Р. Основи квантової механіки. — К. : Либідь, 2002. — 392 с.
• Блохинцев Д. И. Основы квантовой механики. — М. : Наука, 1983. — 664 с.

• Рівні Ландау
• Гармонічний осцилятор
• Осциляції Зенера — Блоха
• Квантовий рух в електричному полі