Коробковий графік

Діаграма розмаху[1][2], коро́бковий гра́фік або гра́фік «я́щик з ву́сами» (англ. box-and-whisker plot, box plot) — засіб візуалізації в описовій статистиці груп числових даних через їх квантилі. Коробковий графік може також мати лінії, які виходять вертикально з коробки (вони називаються вусами), вони вказують величину мінливості поза верхньою та нижньою межами квантиля. Викиди може бути нанесено у вигляді точок.

Рис. 1. Коробковий графік з даними експерименту Майкельсона—Морлі

Коробкові графіки — непараметричні: вони відображають мінливість у вибірці статистичної сукупності, не роблячи ніяких припущень про базовий статистичний розподіл. Віддаль між різними частинами коробки вказують на ступінь дисперсії (розкиданості), асиметрію в даних і відображають викиди. Крім самих точок, вони дозволяють візуально різні статистичні оцінки даних. Коробковий графік може бути як вертикальним так і горизонтальним.

Типи
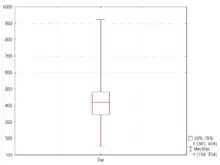
Рис. 2. Коробковий графік з вусами від мінімуму до максимуму
Рис. 3. Такий же коробковий графік з вусами із максимумом 1.5 IQR

Коробка та вуса відображають квартилі: нижня та верхня сторони ящика завжди - це перший (25-й процентиль) і третій квартилі (75-й процентиль), а смужка всередині коробки - другий квартиль (медіана). Але кінці вусів можуть представляти кілька можливих альтернативних значень, серед яких:

  • мінімум та максимум даних[3] як на рисунку 2.
  • найнижче значення даних, який знаходиться ще в межах 1,5 IQR (міжквартильного інтервалу) нижнього квартиля, а найвище значення в межах 1,5 IQR верхнього квартиля [4][5](як показано на рисунку 3)
  • одне стандартне відхилення вище і нижче середніх даних
  • 9-й процентиль і 91-й процентиль
  • 2-й процентиль і 98-й процентиль.

Будь-які дані, що не включено між вусами, повинно бути нанесено на графік ізольованими точки, малим колом або зірочками, але інколи цього не роблять.

Деякі «ящики з вусами» включають додаткові символи, щоб показати середнє значення даних. На деяких ділянках коробкового графіку вуса зображено штрихованою лінією.

Інколи, коробковий графік може бути представлений взагалі без вусів.

Незвичні процентилі 2%, 9%, 91%, 98% іноді використовуються на заштрихованих ділянках вусів та кінцях вусів, щоб показати семи-чисельну описову статистику. Якщо дані мають нормальний розподіл, місця розташування позначень семи статистичних параметрів на графіку будуть рівновіддалено розподілені.

Варіації
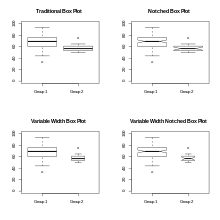
Рис. 4. Коробковий графік з виїмками та змінною шириною
Рис. 5. «Ящик з вусами» та густина ймовірності нормального розподілу

Дві з найбільш поширених варіацій графіку — це зміна ширини ящика та зубчастий механізм. Зміна ширина ящика ілюструє розмір кожної групи даних. Поширений варіант розширення ящика — змінити ширину таким чином, щоб вона була пропорційна квадратному кореню розміру групи[3].

Вуса корисні для грубого припущення щодо суттєвої відмінності медіан; якщо вуса двох ящиків не перекриваються, то це можна сприймати як доказ статистично суттєвої різниці між медіанами.[3] Ширина вус пропорційна міжквантильному діапазону (IQR) і обернено пропорційна квадратному кореню розміру вибірки. Тим не менш, існує невизначеність щодо найбільш відповідного множника (оскільки він може змінюватись в залежності від подібності дисперсій вибірок). Одна з домовленостей полягає у використанні .

Візуалізація

«Ящик з вусами» — це швидкий спосіб вивчення одного або декількох наборів даних у графічному вигляді. «Ящик з вусами» може здатися примітивнішим за оцінку гістограми або ядерну оцінку густини розподілу, але цей метод має деякі переваги. Коробковий графік займає менше місця і тому особливо корисний для порівняння розподілу між кількома групами або наборами даних.

Для кращого розуміння коробкового графіку корисно глянути коробковий графік в порівнянні із функцією густини ймовірності нормального розподілу (теоретично гістограмою) (див. рисунок 5).

Див. також

Джерела
  1. Створення діаграми розмаху// Документація до Microsoft Excell 2019
  2. StatPlus для Windows
  3. McGill, Robert; Tukey, John W.; Larsen, Wayne A. (February 1978). Variations of Box Plots. The American Statistician 32 (1): 12–16. JSTOR 2683468. doi:10.2307/2683468.
  4. Frigge, Michael; Hoaglin, David C.; Iglewicz, Boris (February 1989). Some Implementations of the Boxplot. The American Statistician 43 (1): 50–54. JSTOR 2685173. doi:10.2307/2685173.
  5. Interquartile Ranges & Outliers. Purple Math. Процитовано 18 квітня 2018.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.