Квадратний корінь

	Квадратний корінь
Формула
Область визначення функції	множина невід'ємних дійсних чиселd
Область значень	множина невід'ємних дійсних чиселd
Зображений на	√
Нотація	Знак кореня
Команда TeX	\sqrt[2]{x}
	Квадратний корінь у Вікісховищі

Квадра́тний ко́рінь з числа $x$ — це число (матриця, функція, оператор тощо), квадрат якого (результат множення на себе) дорівнює $x$ . Квадратний корінь часто називають просто корінь.

Серед чисел, квадрат яких дорівнює додатному числу $x$ , обов'язково є додатне число (крім 0). Це число називається арифметичним значенням квадратного кореня і позначається символом ${\sqrt {x}}$ або як $x^{\frac {1}{2}}$ .

{\sqrt {121}}=11

{\sqrt {9}}=3

Число $-{\sqrt {x}}$ теж є квадратним коренем.

В загальному випадку, коли $x$ — будь-який алгебраїчний вираз, символом ${\sqrt {x}}$ позначається один із коренів, той для якого дійсна частина додатна.

При визначенні квадратного кореня з числа завжди існує дві відповіді. Винятком є число 0. Це показують ставлячи перед відповіддю одночасно знак плюс та мінус[1].

Квадратний корінь як елементарна функція

Графік функції

y = \sqrt x

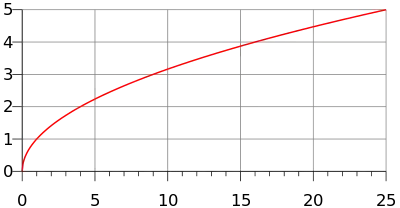
Квадратний корінь є елементарною функцією і є окремим випадком степеневої функції $x α$ з $α = 1/2$ . Арифметичний квадратний корінь є гладким при $x > 0$ , в нулі ж він неперервний справа, але не диференційовний.[2]

Як функція комплексної змінної корінь — двозначна функція, листи якої з'єднуються в нулі.

У геометричному сенсі, функція f(x) = √x квадратного кореня співвідносить площу квадрата до довжини його сторони.

Для всіх дійсних чисел x

{\sqrt {x^{2}}}=\left|x\right|={\begin{cases}x,&{\mbox{if }}x\geq 0\\-x,&{\mbox{if }}x<0.\end{cases}}

(див. абсолютне значення)

Для всіх не від'ємних дійсних чисел x і y,

{\sqrt {xy}}={\sqrt {x}}{\sqrt {y}}

і

{\sqrt {x}}=x^{1/2}.

Функція квадратного кореня є неперервною для всіх не від'ємних значень x і диференційована для всіх додатних x. Якщо f позначає функцію квадратного кореня, тоді її похідна буде мати наступний вигляд:

f'(x)={\frac {1}{2{\sqrt {x}}}}.

Ряд Тейлора для √1 + x при x = 0 буде збіжним для $\left|x\right|$ ≤ 1 і буде визначений наступним чином

{\sqrt {1+x}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{(1-2n)(n!)^{2}(4^{n})}}x^{n}=1+\textstyle {\frac {1}{2}}x-{\frac {1}{8}}x^{2}+{\frac {1}{16}}x^{3}-{\frac {5}{128}}x^{4}+\dots ,

Квадратний корінь не від'ємного числа використовується для визначення Евклідової норми (і відстані), а також у таких узагальненнях як Гільбертів простір. Вона визначає важливе поняття стандартного відхилення, що використовується в теорії ймовірностей і статистиці.

Узагальнення

Квадратні корені вводяться як розв'язок рівнянь виду $x\circ x=a$ і для інших об'єктів: матриць[3][4], функцій[5][6], операторів[7][8] тощо. Операцією $\circ$ при цьому можуть бути достатньо довільні мультиплікативні операції, наприклад, суперпозиція.

В алгебрі використовується наступне формальне визначення: нехай $(G,\cdot )$ — групоїд і $a\in G$ . Елемент $x\in G$ називається квадратним коренем з $\ a$ якщо $\ x\cdot x=a$ .

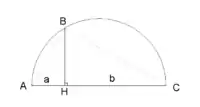
Квадратний корінь в елементарній геометрії

Квадратні корені тісно пов'язані з елементарною геометрією: якщо дано відрізок довжиною 1, то з допомогою циркуля та лінійки можна можна побудувати ті і тільки ті відрізки, довжина яких записується виразами, що містять цілі числа, знаки чотирьох дій арифметики, квадратні корені і нічого крім цього.[9]

Квадратний корінь в інформатиці

У багатьох мовах програмування функціонального рівня (а також мовах розмітки типу LATEX) функція квадратного кореня позначається як sqrt (від англ. square root «квадратний корінь»).

Алгоритми знаходження квадратного кореня

Знаходження або обчислення квадратного кореня заданого числа називається добуванням (квадратного) кореня.

Розклад у ряд Тейлора

{\sqrt {1+x}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{(1-2n)(n!)^{2}(4^{n})}}x^{n}=1+\textstyle {\frac {1}{2}}x-{\frac {1}{8}}x^{2}+{\frac {1}{16}}x^{3}-{\frac {5}{128}}x^{4}+\dots ,\!

при

|x|\leqslant 1

.

Груба оцінка

Багато алгоритмів обчислення квадратних коренів з додатного дійсного числа $S$ потребують деякого початкового значення. Якщо початкове значення занадто далеко від справжнього значення кореня, обчислення сповільнюються. Тому корисно мати грубу оцінку, яка може бути дуже неточною, але легко обчислюватися. Якщо $S \geq 1$ , нехай $D$ буде кількістю цифр $S$ зліва від десяткової коми. Якщо $S < 1$ , нехай $D$ буде кількістю нулів, які йдуть підряд, справа від десяткової коми, взяту зі знаком мінус. Тоді груба оцінка матиме вигляд:

Якщо

D

непарне,

D = 2 n + 1

, тоді використовуємо

{\sqrt {S}}\approx 2\cdot 10^{n}.

Якщо

D

парне,

D = 2 n + 2

, тоді використовуємо

{\sqrt {S}}\approx 6\cdot 10^{n}.

Два і шість використовуються тому, що ${\sqrt {\sqrt {1\cdot 10}}}={\sqrt[{4}]{10}}\approx 2\,$ і ${\sqrt {\sqrt {10\cdot 100}}}={\sqrt[{4}]{1000}}\approx 6\,.$

При роботі в двійковій (яка використовується комп'ютерами), слід використовувати іншу оцінку $2^{\left\lfloor D/2\right\rfloor }$ (тут $D$ — кількість двійкових цифр).

Геометричне добування квадратного кореня

$|BH|={\sqrt {|AH|\cdot |HC|}}$

Зокрема, якщо $\!|AH|=1$ , а $\!|HC|=x$ , то $|BH|={\sqrt {x}}$ [10]

Ітераційний аналітичний алгоритм

${\begin{cases}x_{0}=a\\x_{n+1}={\dfrac {1}{2}}\left(x_{n}+{\dfrac {a}{x_{n}}}\right)\end{cases}}$

тоді $\lim _{n\to \infty }x_{n}={\sqrt {a}}$ .

Квадратні корені від'ємних і комплексних чисел

Перший виток комплексного квадратного кореня

Другий виток комплексного квадратного кореня

Ріманова поверхня квадратного кореня, показує як ці два витки виглядають разом

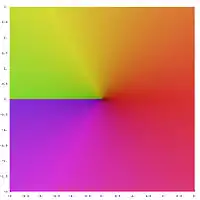
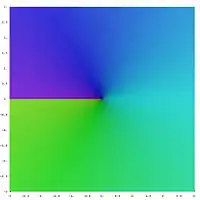
Квадрат будь-якого додатного або від'ємного числа буде додатнім, а квадрат 0 це 0. Тому, від'ємне число не може мати квадратного кореня у вигляді дійсного числа. Однак, існує можливість представити його і вести розрахунки у вигляді спеціальних чисел, що називаються комплексними числами, коли не немає рішення для квадратного кореня від'ємних чисел. Для цього вводиться поняття нового числа, що позначається як i (іноді як j, особливо в контексті розрахунку електричного струму де літера "i" традиційно позначає електричний струм) і називається уявною одиницею, що визначена таким чином, що i² = −1. Використовуючи цю нотацію, ми будемо вважати що i це результат квадратного кореня від −1, але зауважимо, що ми також можемо мати ситуацію, що (−i)² = i² = −1 тому −i також є квадратним коренем від −1. Загальноприйнято, що головним квадратним коренем від −1 є i, або в більш загальному випадку, якщо x є будь-яке невід'ємне число, тоді головним квадратним коренем числа −x є

{\sqrt {-x}}=i{\sqrt {x}}.

Права частина і насправді є квадратним коренем від −x, оскільки

(i{\sqrt {x}})^{2}=i^{2}({\sqrt {x}})^{2}=(-1)x=-x.

Для будь-якого не нульового комплексного числа z існує рівно два числа w, таких що w² = z: головний (позитивний) квадратний корінь z, і його негативний варіант.

Квадратний корінь уявного числа

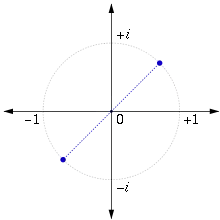
Квадратні корені числа i в комплексній площині

Квадратний корінь числа $i$ буде наступним

{\sqrt {i}}={\frac {1}{2}}{\sqrt {2}}+i{\frac {1}{2}}{\sqrt {2}}={\frac {\sqrt {2}}{2}}(1+i).

Цей можна отримати алгебраїчним шляхом знайшовши дійсні числа a і b, такі що

i=(a+bi)^{2}

або еквівалентно

i=a^{2}+2abi-b^{2}.

Це приводить до появи системи двох рівнянь

{\begin{cases}2ab=1\!\\a^{2}-b^{2}=0\!\end{cases}}

що мають наступне рішення

a=b=\pm {\frac {\sqrt {2}}{2}}.

Якщо вибрати з них головний (додатній) корень, отримаємо

a=b={\frac {\sqrt {2}}{2}}.

Результат також можна отримати, якщо використати формулу Муавра і задати

i=\cos \left({\frac {\pi }{2}}\right)+i\sin \left({\frac {\pi }{2}}\right),

що приводить до

{\begin{aligned}{\sqrt {i}}&=\left(\cos \left({\frac {\pi }{2}}\right)+i\sin \left({\frac {\pi }{2}}\right)\right)^{\frac {1}{2}}\\&=\cos \left({\frac {\pi }{4}}\right)+i\sin \left({\frac {\pi }{4}}\right)\\&={\frac {\sqrt {2}}{2}}+i{\frac {\sqrt {2}}{2}}\\&={\frac {\sqrt {2}}{2}}(1+i).\\\end{aligned}}

Див. також

Примітки

Г. Корн, Т. Корн «Бёрд Дж. Инженерная математика: Карманный справочник/ Пер. с. англ. — М.: Издательский дом „Додэка- XXI“,2008. — 544 с.»(рос.)
Фихтенгольц, 1962, гл. 2, § 1.
Гантмахер Ф. Р. Теория матриц. — 2 изд. — Москва : Наука, 1967. — 576 с. — ISBN 5-9221-0524-8.(рос.)
Воеводин В., Воеводин В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. — Спб : БХВ-Петербург, 2006.(рос.)
Ершов Л. В., Райхмист Р. Б. Построение графиков функций. — Москва : Просвещение, 1984.(рос.)
Каплан И. А. Практические занятия по высшей математике. — Харьков : Изд-во ХГУ, 1966.(рос.)
Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. — Москва : Мир, 1983.(рос.)
Халмош П. Гильбертово пространство в задачах. — Москва : Мир, 1970.(рос.)
Курант, 2000, Глава III Геометрические построения. Алгебра числовых полей.
Курант, 2000, с. 148.

Посилання

Алгоритми обчислення квадратного кореня(англ.)
A geometric view of the square root algorithm(англ.)
Соловьев Ю., Старый алгоритм(рос.)

Література

Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Москва : Наука, 1962. — Т. 1. — 607 с.(рос.)
Курант Р., Роббинс Г. Что такое математика?. — МЦНМО, 2000.(рос.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Г. Корн, Т. Корн «Бёрд Дж. Инженерная математика: Карманный справочник/ Пер. с. англ. — М.: Издательский дом „Додэка- XXI“,2008. — 544 с.»(рос.)

[FOOTNOTEФихтенгольц1962гл.&nbsp;2,_§&nbsp;1-2] Фихтенгольц, 1962, гл. 2, § 1.

[3] Гантмахер Ф. Р. Теория матриц. — 2 изд. — Москва : Наука, 1967. — 576 с. — ISBN 5-9221-0524-8.(рос.)

[4] Воеводин В., Воеводин В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. — Спб : БХВ-Петербург, 2006.(рос.)

[5] Ершов Л. В., Райхмист Р. Б. Построение графиков функций. — Москва : Просвещение, 1984.(рос.)

[6] Каплан И. А. Практические занятия по высшей математике. — Харьков : Изд-во ХГУ, 1966.(рос.)

[7] Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. — Москва : Мир, 1983.(рос.)

[8] Халмош П. Гильбертово пространство в задачах. — Москва : Мир, 1970.(рос.)

[FOOTNOTEКурант2000Глава_III_Геометрические_построения._Алгебра_числовых_полей-9] Курант, 2000, Глава III Геометрические построения. Алгебра числовых полей.

[FOOTNOTEКурант2000148-10] Курант, 2000, с. 148.