Криволінійні координати

Криволінійні системи координат

Полярна система координат на площині

Виходячи з декартової системи координат, можна визначити криволінійну систему координат, тобто, наприклад, для тривимірного простору числа $(x^{1},x^{2},x^{3})$ , зв'язаних із декартовими координатами $(x,y,z)$ співідношеннями:

x^{1}=x^{1}(x,y,z),\qquad x^{2}=x^{2}(x,y,z),\qquad x^{3}=x^{3}(x,y,z)

,

де всі функції однозначні і неперервно диференційовані, причому якобіан:

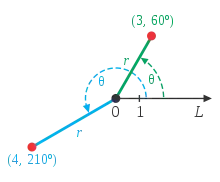
{\frac {\partial (x^{1},x^{2},x^{3})}{\partial (x,y,z)}}\neq 0

.

Прикладом криволінійної системи координат на площині є полярна система координат, в якій положення точки задається двома числами: відстанню $\rho$ між точкою та початком координат, і кутом $\varphi$ між променем, який сполучає початок координат із точкою та обраною віссю. Декартові та полярні координати точки зв'язані між собою формулами:

x=\rho \sin \varphi

,

y=\rho \cos \varphi

,

Для тривимірного простору популярні циліндрична та сферична системи координат. Так, положення літака в просторі можна задати трьома числами: висотою, відстанню до точки на поверхні Землі, над якою він пролітає, та кутом між напрямком на літак і напрямком на північ. Таке задання відповідає циліндричній системі координат, Альтернативно, положення літака можна задати відстанню до нього та двома кутами: полярним та азимутальним. Таке задання відповідає сферичній системі координат.

Різноманітність систем координат не вичерпується наведеними. Існує дуже багато криволінійних систем координат, зручних для використання при розв'язуванні тієї чи іншої математичної задачі.

Властивості

Кожне з рівнянь $x^{i}=x^{1}(x,y,z)={\text{const}}$ , задає координатну площину. Перетин двох координатних площин із різними i задає координатну лінію. Кожна точка простору визначається перетином трьох координатних площин.

Важливими характеристиками криволінійних систем координат є довжина елемента дуги й елемента об'єму у них. Ці величини використовуються при інтегруванні. Довжина елементу дуги задається квадратичною формою:

ds^{2}=dx^{2}+dy^{2}+dz^{2}=\sum _{j=1}^{3}\sum _{k=1}^{3}g_{ik}(x^{1},x^{2},x^{3})dx^{j}dx^{k}

,

де

g_{jk}(x^{1},x^{2},x^{3})=\left[{\frac {\partial x}{x^{j}}}{\frac {\partial x}{x^{k}}}+{\frac {\partial y}{x^{j}}}{\frac {\partial y}{x^{k}}}+{\frac {\partial z}{x^{j}}}{\frac {\partial z}{x^{k}}}\right]_{(x^{1},x^{2},x^{3})}

$g_{jk}$ є компонентами метричного тензора.

Елемент об'єму дорівнює в криволінійній системі координат

dV={\frac {\partial (x^{1},x^{2},x^{3})}{\partial (x,y,z)}}dx^{1}dx^{2}dx^{3}

.

Квадрат якобіана дорівнює детермінанту від метричного тензора:

\left({\frac {\partial (x^{1},x^{2},x^{3})}{\partial (x,y,z)}}\right)^{2}=\det[g_{jk}]=g

.

Система координат називається правою, якщо дотичні до координатних ліній, направлені в бік зростання відповідних координат, утворюють праву трійку векторів.

При описі векторів у криволінійній системі координат зручно користуватися локальним базизом, визначеним у кожній точці.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.