Локально зв'язаний простір

Наступні твердження є еквівалентними:

• Топологічний простір ${\displaystyle X}$ є локально зв'язаним, згідно означення даного вище.
• Будь-яка компонента зв'язності довільного відкритого підпростору простору ${\displaystyle X}$ є відкритою підмножиною.
• Будь-яка відкрита підмножина, як топологічний простір, є диз'юнктивним об'єднанням своїх компонент зв'язності із диз'юнктивною топологією.

Припустимо, що ${\displaystyle X}$ є локально зв'язаним, ${\displaystyle U\subset X}$ — відкрита підмножина і ${\displaystyle U_{0}\subset U}$ — її компонента зв'язності. Нехай ${\displaystyle x\in U_{0}}$. Тоді також ${\displaystyle x\in U}$ і тому існує відкритий зв'язаний окіл ${\displaystyle U_{x,0}\subset U}$ точки ${\displaystyle X}$. Цей окіл має бути підмножиною ${\displaystyle U_{0}}$, оскільки ${\displaystyle U_{0}}$ є компонентою зв'язності ${\displaystyle U}$.

Тому ${\displaystyle U_{0}={\underset {x\in U_{0}}{\cup }}U_{x,0}}$ є об'єднанням відкритих множин і теж є відкритою множиною. Тому з першого означення випливає друге.

Припустимо тепер, що кожна компонента зв'язності довільної відкритої підмножини ${\displaystyle U}$ теж є відкритою множиною. Зокрема ми отримуємо відрите покриття простору ${\displaystyle U}$ компонентами зв'язності. Формуючи перетини із цим покриттям довільної відкритої підмножини в ${\displaystyle U}$ отримуємо, що довільна така підмножина є диз'юнктивним об'єднанням відкритих підмножин компонент зв'язності. Таким чином із другого означення випливає перше.

Припустимо, що будь-яка відкрита підмножина є диз'юнктивним об'єднанням своїх компонент зв'язності. Нехай ${\displaystyle x}$ — точка і ${\displaystyle U_{x}\supset \{x\}}$ — її окіл. За означенням ${\displaystyle U_{x}}$ містить відкритий окіл точки ${\displaystyle x}$ і згідно припущення цей окіл є диз'юнктивним об'єднанням своїх компонент зв'язності, що є відкритими підмножинами. Одна з цих підмножин містить ${\displaystyle x}$ і задовольняє вимоги з означення локальної зв'язності.

• Будь-яка відкрита підмножина локально зв'язаного простору є локально зв'язаним простором.
• Будь-яка компонента зв'язності локально зв'язаного простору є відкрито-замкнутою.
• Будь-який компактний локально зв'язаний простір має скінченну кількість компонент зв'язності.
• Якщо простір ${\displaystyle X}$ є локально зв'язаним, а відображення ${\displaystyle f:X\to Y}$ — неперервне, відкрите і сюр'єктивне. Тоді ${\displaystyle Y}$ теж є локально зв'язаним.

Нехай ${\displaystyle f(x)\in Y}$ — довільна точка і ${\displaystyle U}$ — будь-який окіл точки ${\displaystyle f(x)}$. Із неперервності відображення випливає, що ${\displaystyle f^{-1}(U)}$ є околом точки ${\displaystyle x}$. Згідно локальної зв'язаності простору ${\displaystyle X}$ існує відкритий зв'язаний окіл ${\displaystyle V}$ точки ${\displaystyle x}$, що є підмножиною ${\displaystyle f^{-1}(U)}$. Зважаючи на неперервність і відкритість відображення ${\displaystyle f}$, множина ${\displaystyle f(V)}$ теж є відкритою і зв'язаною і також очевидно ${\displaystyle f(x)\in f(V)\subset U}$. Тобто вимоги локальної зв'язаності ${\displaystyle Y}$ виконуються.

• Нехай ${\displaystyle \{X_{i}\}_{i\in I}}$ — деяка сім'я топологічних просторів і їх добуток ${\displaystyle X=\prod _{i\in I}X_{i}}$ є локально зв'язаним. Тоді усі простори ${\displaystyle X_{i}}$ теж є локально зв'язаними, оскільки кожна проекція на множник є неперервним відкритим сюр'єктивним відображенням.
• Довільний скінченний добуток локально зв'язаних просторів є локально зв'язаним простором. Для нескінченного добутку це твердження не є правильним. Прикладом може бути простір ${\displaystyle \{0,1\}^{\mathbb {N} }}$.
• Натомість якщо ${\displaystyle \{X_{i}\}_{i\in I}}$ є сім'єю локально зв'язаних і також зв'язаних топологічних просторів, то їх добуток ${\displaystyle X=\prod _{i\in I}X_{i}}$ є локально зв'язаним.
• Фактор-простір локально зв'язаного топологічного простору теж є локально зв'язаним.

Нехай ${\displaystyle q:X\to Y}$ — відображення на фактор-простір і ${\displaystyle V\subseteq Y}$ — відкритий окіл точки ${\displaystyle y\in Y}$. Позначимо ${\displaystyle C(y)}$ компоненту зв'язності ${\displaystyle V}$, що містить точку ${\displaystyle y}$; достатньо довести, що ${\displaystyle C(y)}$ є відкритою підмножиною ${\displaystyle Y}$. Для цього достатньо довести, що ${\displaystyle C=q^{-1}(C(y))}$ є відкритою підмножиною ${\displaystyle X}$. Нехай ${\displaystyle x\in C}$. Оскільки ${\displaystyle X}$ є локально зв'язаним, компонента зв'язності ${\displaystyle U_{x}}$ точки ${\displaystyle x}$ у ${\displaystyle q^{-1}(V)}$ є відкритою і підмножина ${\displaystyle q(U_{x})\subseteq V}$ є зв'язаною; тому ${\displaystyle q(U_{x})\subseteq C(y)}$ (оскільки ${\displaystyle C(y)}$ є компонентою зв'язності що містить ${\displaystyle q(x)}$). Тому ${\displaystyle U_{x}\subseteq q^{-1}(C(y))=C}$, і точка ${\displaystyle x}$ є внутрішньою у ${\displaystyle C}$. Зважаючи на довільність вибору точки ${\displaystyle x}$ множина ${\displaystyle C}$ є відкритою, що завершує доведення.

• Простір ${\displaystyle X}$ є локально зв'язаним тоді і тільки тоді, коли для будь-якого сімейства ${\displaystyle \{X_{i}\}_{i\in I}}$ підмножин ${\displaystyle X}$ має місце включення ${\displaystyle \partial \left(\bigcup _{i\in I}X_{i}\right)\subset {\overline {\bigcup _{i\in I}\partial (X_{i})}}}$, де ${\displaystyle \partial }$ — межа множини, a ${\displaystyle {\overline {A}}}$ позначає замикання множини ${\displaystyle A}$.

Синус тополога.

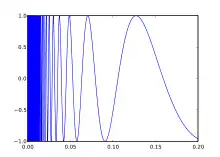
• Для додатного цілого числа ${\displaystyle n}$, евклідів простір ${\displaystyle \mathbb {R} ^{n}}$ є локально зв'язаним і зв'язаним.
• Підпростір ${\displaystyle [0,1]\cup [2,3]}$ дійсної прямої ${\displaystyle \mathbb {R} ^{1}}$ є локально зв'язаним але не зв'язаним.
• Стандартним прикладом простору, що є зв'язаним але не локально зв'язаним є синус тополога.[1] Цей простір є підмножиною точок на площині ${\displaystyle T=\left\{\left.\left(x,\sin {\frac {1}{x}}\right)\right|x\in ]0,1]\right\}\cup \{(0,0)\}}$ із індукованою топологією.
• Простір ${\displaystyle \mathbb {Q} }$ не є локально зв'язаним і не є зв'язаним.
• Будь-який локально лінійно зв'язаний простір є локально зв'язаним.
• Зліченна множина із кофінітною топологією (в якій замкнутими множинами є скінченні множини і весь простір) є локально зв'язаною але не локально лінійно зв'язаною.[2]
• Будь-який повний метричний локально зв'язаний простір є локально лінійно зв'язаним (теорема Мазуркевича — Мура — Менгера)

Нескінченна мітла. У замкнутій нескінченній мітлі додається теж весь відрізок від початку координат до точки (1,0)

Простір X називається слабко локально зв'язаним у точці x якщо для кожного околу V точки x існує зв'язаний але не обов'язково відкритий окіл N точки x, що є підмножиною V .

Простір X називають слабко локально зв'язаним якщо він є слабко локально зв'язаним у всіх точках x. Насправді проте поняття слабкої локальної зв'язаності для всього простору є еквівалентним поняттю локальної зв'язаності.

Теорема

Якщо X є слабко локально зв'язаним простором, то він є локально зв'язаним.

Доведення

Нехай U є відкритою підмножиною X, C — компонента зв'язності U і x — елемент C. Тоді існує зв'язаний окіл A точки x у X, що є підмножиною U. Оскільки A є зв'язаною підмножиною і містить x, A є підмножиною C. Згідно з означенням околу існує відкрита множина V , що містить x і є підмножиною A і тому підмножиною C. Тому точка x є внутрішньою у C. Оскільки точка x була довільною то C є відкритою множиною. Тобто довільна компонента зв'язності довільної відкритої підмножини є відкритою і тому X є локально зв'язаним.

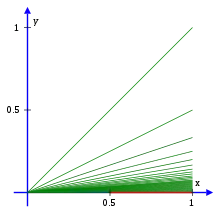
Натомість простір може бути слабко локально зв'язаним у точці але не локально зв'язаним у ній. Прикладом може бути простір утворений із нескінченної послідовності просторів, що називаються замкнутою нескінченною мітлою. Замкнутою нескінченною мітлою називається об'єднання відрізків на площині, що сполучають точку (0,0) із точками з координатами (1, 1/n) для всіх натуральних чисел n, а також з точкою (1,0).

Нескінченна послідовність отримується якщо замість точки (0,0) брати послідовно точки виду ((n-1)/n,0) для всіх натуральних чисел і пропорційно зменшити замкнуту нескінченну мітлу так, щоб горизонтальний відрізок мав довжину ${\displaystyle {\frac {n}{n+1}}-{\frac {n-1}{n}}}$.

Вставивши послідовно ці простори у відповідні точки отримаємо зв'язаний топологічний простір , що є об'єднанням нескінченної кількості пропорційно зменшених копій замкнутої нескінченної мітли. У точці (1,0) цей прості є слабко локально зв'язаним але не є локально зв'язаним[3].

• Зв'язаний простір
• Локально лінійно зв'язаний простір

• Локально зв'язаний простір у проекті nLab.

• Gaal, Steven A.(1966), Point set topology, New York: Dover Publications, ISBN 978-0-486-47222-5 (англ.)
• Isadore Singer, John A. Thorpe (1967), Lecture Notes on Elementary Geometry and Topology, Springer-Verlag ISBN 0-387-90202-3 (англ.)
• Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978]. Counterexamples in Topology (вид. Dover reprint of 1978). Mineola, NY: Dover Publications, Inc. ISBN 978-0-486-68735-3. MR 1382863.(англ.)