Матроїд

Матроїд — пара ${\displaystyle (X,I)}$, де ${\displaystyle X}$ — скінченна множина, звана носієм матроїда, а ${\displaystyle I}$ — деяка множина підмножин ${\displaystyle X}$, звана сімейством незалежних множин, тобто ${\displaystyle I\subset }$ ${\displaystyle 2^{X}}$. При цьому повинні виконуватися наступні умови:

1. ${\displaystyle \varnothing \in I}$
2. Якщо ${\displaystyle A\in I}$ та ${\displaystyle B\subset A}$, то ${\displaystyle B\in I}$
3. Якщо ${\displaystyle A,B\in I}$ і потужність A більша потужності B, то існує ${\displaystyle x\in A\setminus B}$ такий, що ${\displaystyle B\cup \{x\}\in I}$

Базами матроїда називаються максимальні по включенню незалежні множини. Підмножини ${\displaystyle X}$, які не належать ${\displaystyle I}$, називаються залежними множинами. Мінімальні по включенню залежні множини називаються циклами матроїда, це поняття використовується в альтернативному визначенні матроїда.

Матроїд — пара ${\displaystyle (X,C)}$, де ${\displaystyle X}$ — носій матроїда, а ${\displaystyle C}$ — сімейство непустих підмножин ${\displaystyle X}$, зване множиною Циклів матроїда, для яких виконуються наступні умови:[1]

1. Жоден цикл не є підмножиною іншого.
2. Якщо ${\displaystyle x\in C_{1}\cap C_{2}}$, то ${\displaystyle C_{1}\cup C_{2}\setminus \{x\}}$ містить цикл.

Нехай ${\displaystyle (P,\leq )}$ — частково впорядкована множина. ${\displaystyle H:P\to P}$ — замикання в ${\displaystyle (P,\leq )}$, якщо

1. Для будь-якого x з P: ${\displaystyle H(x)\geq x}$
2. Для будь-яких x,y з P: ${\displaystyle x\leq y\Rightarrow H(x)\leq H(y)}$
3. Для будь-якого x з P: ${\displaystyle H\left(H\left(x\right)\right)=H(x)}$

Розглянемо ${\displaystyle (P,\leq )=(2^{S},\leq )}$ випадок, коли частково впорядкована множина — булева алгебра. Нехай ${\displaystyle A\to H(A)}$ — замикання${\displaystyle A\subset S}$.

1. Замикання правильне (аксіома правильного замикання), якщо ${\displaystyle (p\not \in A,p\in H(A\cup \left\{q\right\}))\Rightarrow q\in H(A\cup \left\{p\right\})}$
2. Для будь-якого ${\displaystyle A\subset S}$ існує таке ${\displaystyle B\subset A}$, що
   1. ${\displaystyle |B|<+\infty }$
   2. ${\displaystyle H\left(B\right)=H\left(A\right)}$

Пара ${\displaystyle (S,A\to H(A))}$, де ${\displaystyle A\to H(A)}$ — правильне замикання на ${\displaystyle (2^{S},\leq )}$, називається матроїдом.

1. Універсальний матроїд U_nk. Множина X має потужність n, незалежними множинами є підмножини потужністю не більше k. Бази — підмножини потужністю k.
2. Матроїд циклів графу. Множина X — множина ребер графу, незалежні множини — ациклічні підмножини цих ребер, цикли — прості цикли графу. Базами є кістякові дерева графу. Матроїд називається 'графічним', якщо він є матроїдом циклів деякого графу.[2]
3. Матроїд підмножин множини ребер графу, таких що видалення підмножини залишає граф зв'язаним.
4. Матроїд коциклів графу. Множина X — множина ребер, коцикли — мінімальні множини, видалення яких призводить до втрати зв'язності графу. Матроїд називається 'кографічним', якщо він є матроїдом коциклів деякого графу.[2]
5. Матричний матроїд. Сімейство всіх лінійно незалежних підмножин будь-якої скінченної множини векторів довільного непорожнього векторного простору є матроїдом.

Визначимо множину E, як таку, що складається з {1, 2, 3, .., n} — номерів стовпців деякої матриці, а множину I, як таку, яка складається з підмножин E, таких що вектори, які визначаються ними, є лінійно незалежними над полем дійсних чисел R. Виникає питання — якими властивостями володіє побудована множина I?

1. Множина I — непорожня. Навіть якщо вихідна множина E була б порожньою — E = ∅, то I буде складатися з одного елемента — множини, що містить порожню множину I = ∅.
2. Будь-яка підмножина будь-якого елемента множини I також буде елементом цієї множини. Ця властивість зрозуміла — якщо деякий набір векторів лінійно незалежний над полем, то лінійно незалежним буде також будь-який його піднабір.
3. Якщо A, B ∈ I, причому|A|=|B|+ 1, тоді існує елемент x ∈ A — B, такий що B ∪ {x} ∈ I.

Доведемо, що в розглянутому прикладі множина лінійно незалежних стовпців дійсно є матроїдом. Для цього достатньо довести третю властивість з визначення матроїда. Проведемо доведення методом від протилежного.

Доведення. Нехай A, B ∈ I і|A|=|B|+ 1. Нехай W буде простором векторів, які охоплюють A ∪ B. Зрозуміло, що його розмірність буде не меншою|A |. Припустимо, що B ∪ {x} буде лінійно залежною для всіх x ∈ A — B (тобто третя властивість не буде виконуватися). Тоді B утворює базис в просторі W. З цього випливає, що|A|≤ dim W ≤|B |. Але, так як за умовою A і B складаються з лінійно незалежних векторів і|A |>|B |, одержуємо суперечність. Така множина векторів буде матроїдом.

• Двоїстим до даного матроїду називається матроїд, носій якого збігається з носієм даного матроїда, а бази — з доповненням баз даного матроїда до носія. Тобто X^* = X, а безліч баз двоїстого матроїда — це множина таких B^*, що B^* = X\B, де B — база даного матроїда.
• Циклом в матроїді називається така множина A ⊂ X, що A ∉ I, і для будь-якого B ⊂ A, якщо B ≠ A, то B ∈ I
• Рангом матроїда називається потужність його баз. Ранг тривіального матроїда дорівнює нулю.

Матроїд Фано

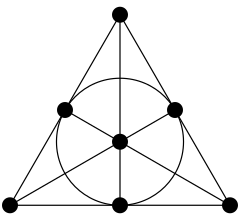
Матроїди з невеликим числом елементів часто зображують у вигляді діаграм. Точки — це елементи основної множини, а криві «протягнуті» через кожен трьохелементний ланцюг (3-element circuit). Діаграма показує 3-ранговий матроїд, званий матроїдом Фано, приклад якого з'явився в 1935 в статті Уїтні (Whitney).

Назва виникла з того факту, що матроїд Фано являє собою проективну площину другого порядку, відому як площина Фано, чиє координатне поле — це двохелементне поле. Це означає, що матроїд Фано — це векторний матроїд, пов'язаний з сімома ненульовими векторами в тривимірному векторному просторі над полем двох елементів.

З проективної геометрії відомо, що матроїд Фано не може бути представлений довільною множиною векторів в дійсному або комплексному векторному просторі (або в будь-якому векторному просторі над полем, характеристики якого відрізняються від 2).

• Всі бази матроїда мають однакову потужність.
• Матроїд однозначно задається носієм і базами.
• Цикл не може бути підмножиною іншого циклу
• Якщо ${\displaystyle C_{1}}$ і ${\displaystyle C_{2}}$ — цикли, то для будь-якого ${\displaystyle x\in C_{1}\cap C_{2}:C_{1}\cup C_{2}\setminus \{x\}}$ містить цикл
• Якщо ${\displaystyle B}$ — база і ${\displaystyle x\notin B}$, то ${\displaystyle B\cup \{x\}}$ містить рівно один цикл.

• Матроїди добре описують клас задач, які допускають «жадібне» рішення. Див. жадібний алгоритм Радо-Едмондса.
• Матроїди в комбінаторній оптимізації.

• Орієнтований матроїд