Булеан

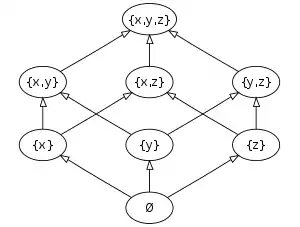
Нехай ${\displaystyle S\ {\mathcal {=}}\ \{x,y,z\}}$. Тоді підмножинами ${\displaystyle S}$ є:

• ${\displaystyle \varnothing }$ (або ${\displaystyle \emptyset }$) — порожня множина
• ${\displaystyle \{x\}}$
• ${\displaystyle \{y\}}$
• ${\displaystyle \{z\}}$
• ${\displaystyle \{x,y\}}$
• ${\displaystyle \{x,z\}}$
• ${\displaystyle \{y,z\}}$
• ${\displaystyle \{x,y,z\}}$

Отже, булеаном множини ${\displaystyle S}$ є множина ${\displaystyle {\mathcal {P}}(S)=}$ ${\displaystyle \{}$${\displaystyle \varnothing }$, ${\displaystyle \{x\}}$, ${\displaystyle \{y\}}$, ${\displaystyle \{z\}}$, ${\displaystyle \{x,y\}}$, ${\displaystyle \{x,z\}}$, ${\displaystyle \{y,z\}}$, ${\displaystyle \{x,y,z\}}$${\displaystyle \}}$.

Якщо ${\displaystyle S}$ — скінченна множина та ${\displaystyle |S|=n}$, тоді кількість підмножин ${\displaystyle S}$ дорівнює ${\displaystyle |{\mathcal {P}}(S)|=2^{n}}$. Цей аспект, який є передумовою до позначення ${\displaystyle 2^{S}}$, може бути представлений наступним чином:

Спершу упорядкуємо елементи ${\displaystyle S}$ будь-яким чином. Ми записуємо кожну підмножину ${\displaystyle S}$ у вигляді ${\displaystyle \{\omega _{1},\omega _{2},...,\omega _{n}\}}$, де ${\displaystyle \omega _{i},1\leq i\leq n}$, може приймати значення 0 або 1. Якщо ${\displaystyle \omega _{i}=1}$, тоді  ${\displaystyle i}$-ий елемент множини ${\displaystyle S}$ знаходиться у підмножині; в іншому випадку, цей елемент відсутній. Очевидно, кількість різних підмножин, які можна отримати таким чином, дорівнює ${\displaystyle 2^{n}}$.

Діагональний метод Кантора показує, що булеан множини ${\displaystyle S}$ (скінченної або нескінченної) завжди має строго більшу потужність, ніж сама множина ${\displaystyle S}$. Зокрема, теорема Кантора свідчить, що булеан зліченної множини є незліченним. Наприклад, можна утворити бієктивне відображення між булеаном множини натуральних чисел та множиною дійсних чисел.

Булеан множини ${\displaystyle S}$ поряд з операціями об'єднання, перетину та доповнення може розглядатися як приклад булевої алгебри. Можна показати, що будь-яка скінченна булева алгебра є ізоморфною до булевої алгебри булеана скінченної множини. Для нескінченних булевих алгебр ця умова не виконується, але будь-яка нескінченна булева алгебра може бути представлена як підалгебра булеана булевої алгебри (див.: теорема Стоуна про представлення булевих алгебр).

Булеан множини ${\displaystyle S}$ формує абелеву групу по операції симетричної різниці та комутативний моноїд по операції перетину. Отже, можна показати (доводячи дистрибутивність), що булеан формує булеве кільце по цим операціям.

У теорії множин, ${\displaystyle X^{Y}}$ позначає множину усіх функцій із ${\displaystyle Y}$ в ${\displaystyle X}$. ${\displaystyle 2^{S}}$ — множина усіх відображень із ${\displaystyle S}$ у ${\displaystyle 2=\{0,1\}}$. Визначаючи функцію в ${\displaystyle 2^{S}}$ з відповідним прообразом 1, ми бачимо, що відображення між ${\displaystyle 2^{S}}$ та ${\displaystyle {\mathcal {P}}(S)}$ є бієктивним, де кожна функція є характеристичною функцією підмножини ${\displaystyle {\mathcal {P}}(S)}$, у якій вона визначена. Таким чином, ${\displaystyle 2^{S}}$ та ${\displaystyle {\mathcal {P}}(S)}$ можна вважати теоретико-множинно ідентичними.

Це поняття може бути застосоване до вищенаведеного прикладу, де ${\displaystyle S\ {\mathcal {=}}\ \{x,y,z\}}$, щоб побачити ізоморфізм з двійковими числами від 0 до ${\displaystyle 2^{n}-1}$, де ${\displaystyle n}$ — кількість елементів у множині. У ${\displaystyle S}$ "1" на позиції, яка відповідає позиції елемента у множині, позначає присутність цього елемента. Такими чином, ${\displaystyle \{x,y\}=\{1,1,0\}}$.

Для всієї множини отримуємо:

• ${\displaystyle \varnothing =000_{2}=0_{10}}$
• ${\displaystyle \{x\}=100_{2}=4_{10}}$
• ${\displaystyle \{y\}=010_{2}=2_{10}}$
• ${\displaystyle \{z\}=001_{2}=1_{10}}$
• ${\displaystyle \{x,y\}=110_{2}=6_{10}}$
• ${\displaystyle \{x,z\}=101_{2}=5_{10}}$
• ${\displaystyle \{y,z\}=011_{2}=3_{10}}$
• ${\displaystyle \{x,y,z\}=111_{2}=7_{10}}$

Для скінченної множини ${\displaystyle S}$ існує рекурсивний алгоритм для знаходження ${\displaystyle {\mathcal {P}}(S)}$.

Визначимо операцію ${\displaystyle {\mathcal {F}}(e,T)=\{X\cup \{e\}|X\in T\}}$.

• Якщо ${\displaystyle S=\varnothing }$, тоді повернемо ${\displaystyle {\mathcal {P}}(S)=\{\varnothing \}}$.

• В іншому випадку:
  • Нехай ${\displaystyle e}$ — будь-який одиничний елемент з ${\displaystyle S}$.
  • Нехай ${\displaystyle T=S\setminus \{e\}}$, де ${\displaystyle S\setminus \{e\}}$ — відносне доповнення ${\displaystyle \{e\}}$ в ${\displaystyle S}$.
  • Повернемо ${\displaystyle {\mathcal {P}}(S)={\mathcal {P}}(T)\cup {\mathcal {F}}(e,{\mathcal {P}}(T))}$.

Булеан тісно пов'язаний з біномом Ньютона. Кількість підмножин потужності ${\displaystyle k}$ у булеані множини, потужність якої ${\displaystyle n}$, є кількістю комбінацій ${\displaystyle C_{n}^{k}}$, яка також називається біноміальним коефіцієнтом.

Наприклад, множина із трьох елементів містить:

• ${\displaystyle C_{3}^{0}=1}$ підмножину з 0 елементами (порожня множина);
• ${\displaystyle C_{3}^{1}=3}$ підмножини з 1 елементом (одиничні підмножини);
• ${\displaystyle C_{3}^{2}=3}$ підмножини з 2 елементами (усі можливі пари одиничних підмножин);
• ${\displaystyle C_{3}^{3}=1}$ підмножину з 3 елементами (уся початкова множина).

Множина підмножин ${\displaystyle S}$, потужність яких менше ніж ${\displaystyle k}$, позначається ${\displaystyle {\mathcal {P}}_{k}(S)}$ або ${\displaystyle {\mathcal {P}}_{<k}(S)}$. Таким чином, множина непорожніх підмножин ${\displaystyle S}$ може бути позначена ${\displaystyle {\mathcal {P}}_{\geq 1}(S)}$.

Справедливо наступне твердження: число підмножин кінцевої множини, яка складається з ${\displaystyle n}$ елементів, дорівнює ${\displaystyle 2^{n}}$. Результат доводиться методом матиматичної індукції. В базі пустої множини ${\displaystyle \varnothing }$(${\displaystyle n=0}$) тільки одна підмножина — вона сама, і ${\displaystyle 2^{0}=1}$. На кроці індукції твердження вважається встановленим для множин потужності ${\displaystyle n}$ та розглядається довільна множина ${\displaystyle M}$ з кардинальним числом ${\displaystyle n+1}$; зафіксувавши деякий елемент ${\displaystyle a_{0}\in M}$, підмножини множини ${\displaystyle M}$ розділяються на два сімейства:

1. ${\displaystyle M_{1}}$, що містить ${\displaystyle a_{0}}$,
2. ${\displaystyle M_{2}}$, що не містить ${\displaystyle a_{0}}$_, тобто є підмножинами множини ${\displaystyle M\setminus \{a_{0}\}}$.

Підмножин другого типу по припущенню індукції ${\displaystyle 2^{n}}$, підмножин першого типу рівно стільки ж, так як підмножина такого типу отримується з деякої єдиної підмножини другого типу додаванням елемента ${\displaystyle a_{0}}$ _{і, отже:}

${\displaystyle 2^{M}=M_{1}\bigcup M_{2}}$ та ${\displaystyle M_{1}\bigcap M_{2}=\varnothing }$.

За індукціонним припущенням ${\displaystyle \left|M_{1}\right|=2^{n}}$ та ${\displaystyle \left|M_{2}\right|=2^{n}}$, тобто:

.${\displaystyle \left|2^{M}\right|=\left|M_{1}\right|+\left|M_{2}\right|=2^{n}+2^{n}=2^{n+1}=2^{\left|M\right|}}$

• Аксіома булеана
• Теорема Кантора
• Континуум-гіпотеза
• Теорія множин
• Алгебра множин

• Weisstein, Eric W., "Power Set", на сайті MathWorld.
• Булеан на сайті PlanetMath.org.
• Булеан на сайті nLab.
• Експоненціал на сайті nLab.