Модулярна група

Модулярна група є дискретною групою перетворень верхньої комплексної півплощини ${\displaystyle H=\{z:\mathrm {Im} \,z>0\}}$ і допускає подання твірними:

${\displaystyle S:z\mapsto -1/z,}$

${\displaystyle T:z\mapsto z+1}$

і співвідношеннями ${\displaystyle S^{2}=(ST)^{3}=1}$, тобто є вільним добутком циклічної групи порядку 2, породженої ${\displaystyle S}$, і циклічної групи порядку 3, породженої ${\displaystyle ST}$.

Для довільного перетворення ${\displaystyle g(z)={\frac {az+b}{cz+d}}}$ з модулярної групи справедлива рівність:

${\displaystyle \mathrm {Im} \,g(z)={\frac {\mathrm {Im} \,z}{|cz+d|^{2}}}.\qquad \qquad (1)}$

Оскільки уявна частина ${\displaystyle z}$ ненульова, а числа ${\displaystyle c}$ і ${\displaystyle d}$ — цілі, не рівні нулю одночасно, то величина ${\displaystyle |cz+d|^{2}}$ відокремлена від нуля (не може бути як завгодно малою). Це означає, що в орбіті будь-якої точки є така, на якій уявна частина досягає свого максимуму.

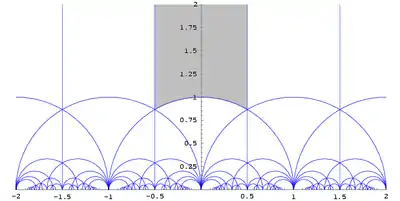
Фундаментальна область (канонічна) модулярної групи — це замкнута область

${\displaystyle D=\{z\in H:|z|\geqslant 1,\;|\mathrm {Re} \,z|\leqslant 1/2\}.}$

Легко перевірити, використовуючи (1), що перетворення модулярної групи не збільшують уявну частину точок з ${\displaystyle D}$. З цього виходить, що для того, щоб дві точки ${\displaystyle z,\;g(z)}$ належали ${\displaystyle D}$, їх уявна частина повинна бути однакова: ${\displaystyle |cz+d|^{2}=1}$. Таким умовам відповідають наступні перетворення і точки:

1. ${\displaystyle g(z)=z,\;z}$ — будь-яка точка;
2. ${\displaystyle g(z)=z-1,\;\mathrm {Re} ,z=1/2;}$
3. ${\displaystyle g(z)=z+1,\;\mathrm {Re} ,z=-1/2;}$
4. ${\displaystyle g(z)=-1/z,\;|z|=1.}$

Зокрема, всі точки області ${\displaystyle D}$ мають тривіальний стабілізатор, окрім трьох:

1. ${\displaystyle \mathrm {St} (i)=\{1,\;S\};}$
2. ${\displaystyle \mathrm {St} (e^{2\pi i/3})=\{1,\;ST,\;(ST)^{2}\};}$
3. ${\displaystyle \mathrm {St} (-e^{-2\pi i/3})=\{1,\;TS,\;(TS)^{2}\}.}$

Крім того, з цього випливає що при факторизації верхньої півплощини по дії модулярної групи внутрішні точки ${\displaystyle D}$ відображаються ін'єктивно, тоді як граничні — склеюються з точками, «дзеркальними» до них відносно прямої ${\displaystyle \mathrm {Re} \,z=0}$.

• Курош А. Г. Теория групп. — 3-е изд. — Москва : Наука, 1967. — 648 с. — ISBN 5-8114-0616-9.(рос.)
• Tom M. Apostol, Modular Functions and Dirichlet Series in Number Theory, Second Edition (1990), Springer, New York ISBN 0-387-97127-0