Мультиграф
В теорії графів мультиграфом (або псевдографом) називають граф, в якому допускається наявність кратних ребер (їх також називають «паралельними»), тобто є ребра, які мають одні й ті ж кінцеві вершини. Таким чином, дві вершини можуть бути з'єднані більш ніж одним ребром (цим мультиграфи відрізняються від гіперграфів, в яких кожне ребро може з'єднувати будь-яке число вершин, а не рівно дві).
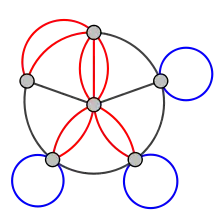
Існує два методи позначення ребер мультиграфу. Деякі говорять, що, як і в випадку графів без кратних ребер, ребро визначається вершинами, які воно з'єднує, але кожне ребро може повторюватися декілька разів. Інші визначають ребра рівноправними з вершинами елементами графу і вони повинні мати власну ідентифікацію.
Неорієнтовані мультиграфи (ребра без власної ідентифікації)
Формально, мультиграфом G називають впорядковану пару G:=(V, E), в якій
- V — множина вершин,
- E — мультимножина невпорядкованих пар вершин. Елементи цієї множини називаються ребрами.
Мультиграфи можна використовувати для подавання можливих повітряних шляхів літака. В цьому випадку мультиграф стає орієнтованим і пара орієнтованих паралельних ребер, які зв'язують міста, показує, що можна летіти в обох напрямках — з міста або в місто.
Деякі автори дозволяють мультиграфам мати петлі, тобто ребра, які з'єднують вершину саму з собою, інші називають такі графи псевдографами, а термін мультиграф залишають для графів без петель.
Орієнтовані мультиграфи (ребра без власної ідентифікації)
Мультиорграф — це орієнтований граф, в якому допустимі кратні дуги, тобто є дуги, які мають однакові початкові і кінцеві вершини.
Мультиорграфом G називається впорядкована пара G:=(V,A), в якій
- V — множина вершин,
- A — мультимножина впорядкованих пар вершин. Елементи цієї множини називають дугами.
Змішаний мультиграф G:=(V,E, A) можна визначити таким же чином, як і змішаний граф.
Орієнтовані мультиграфи (ребра з власною ідентифікацією)
Мультиорграфом G називають впорядковану четвірку G:=(V, A, s, t), в якій
- V — множина вершин,
- A — множина дуг,
- призначає кожній дузі початкову вершину,
- призначає кожній дузі кінцеву вершину.
В теорії категорій невеликі категорії можуть бути визначені як мультиорграфи (з дугами, які мають власну ідентифікацію), оснащені законом побудови і петлями для кожної вершини, які служать лівою і правою ідентифікацією для побудови. У зв'язку з цим в теорії категорій під терміном граф зазвичай розуміють «мультиорграф», мультиорграф який лежить в основі категорії називається базовим орграфом.
Розмітка
Мультиграфи і мультиорграфи підтримують поняття розмітки однаково, однак в цьому випадку немає єдності термінології.
Визначення помічені мультиграфи і помічені мультиорграфи схожі, тому тут вкажемо визначення тільки для мультиорграфу.
Визначення 1: Помічений мультиорграф — це помічений граф з мітками на дугах і вершинах.
Формально: Помічений мультиорграф G — це кортеж з 8 елементів , в якому
- V — множина вершин і A — множина дуг,
- і — кінцевий алфавіт, доступний для розмітки дуг і вершин,
- і — два відображення, які визначають початкову і кінцеву вершини дуги,
- і — два відображення, які описують розмітку вершин і дуг.
Визначення 2: Помічений мультиорграф — помічений орграф з кратними поміченими дугами, тобто дугами з тими ж кінцями і тими ж мітками (це відрізняється від поняття, даного в статті «Розмітка графу»).
Див. також
Примітки
Посилання
- Béla Bollobás. Modern Graph Theory. — Springer, 2002. — ISBN 0-387-98488-7.
- V. K. Balakrishnan. Graph Theory. — McGraw-Hill, 1997. — ISBN 0-07-005489-4.
- Рейнгард Дистель. Теория графов. — Новосибирск: Изд-во Ин-та математики, 2002. — ISBN 5-86134-101-Х.
- Jonathan L Gross, Jay Yellen. Graph Theory and Its Applications. — McGraw-Hill, 1998. — ISBN 0-8493-3982-0.
- Jonathan L Gross, Jay Yellen. Handbook of Graph Theory. — McGraw-Hill, 2003. — ISBN 1-58488-090-2.
- Ф.Харари. Теория графов. — Москва: Едиториал УРСС, 2003. — ISBN 5-354-00301-6.
- Daniel Zwillinger. CRC Standard Mathematical Tables and Formulae. — Chapman & Hall/CRC, 2002. — ISBN 1-58488-291-3.
- Svante Janson, Donald E. Knuth, Tomasz Luczak, Boris Pittel The birth of the giant component // Random Structures and Algorithms. — 1993. — Т. 4, вып. 3. — С. 231—358. — DOI:10.1002/rsa.3240040303.
Зовнішні посилання
- Paul E. Black, Multigraph at the NIST Dictionary of Algorithms and Data Structures.
