Нейтральна вісь
Нейтра́льна вісь (англ. neutral axis) або нейтра́льна лі́нія (в опорі матеріалів) — лінія у поперечному перерізі балки, яка зазнає згинання, у точках якої нормальні напруження, що паралельні до осі балки, дорівнюють нулю. Нейтральна вісь поділяє переріз на дві частини, в одній з яких діють розтягувальні нормальні напруження, а в іншій — стискальні.
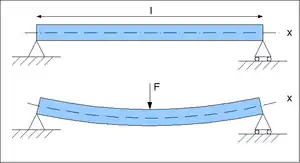
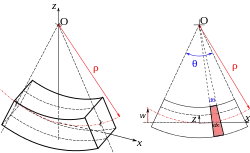

Розподіл нормальних напруження при плоскому згині
Геометричний бік задачі
Для випадку чистого плоского згинання балки із шести внутрішніх силових факторів, які можуть діяти в її поперечних перерізах у загальному випадку не дорівнює нулю тільки згинальний момент M. Вісь балки деформується у площині, що збігається з силовою. Контури поперечних перерізів балки залишаються при цьому плоскими і перпендикулярними до осі балки. На підставі цього можна зробити висновок, що при чистому згині буде справедливою гіпотеза плоских перерізів як і при розтягу-стисканні та крученні.
Виділимо елемент балки двома суміжними поперечними перерізами, що розташовані один від одного на відстані dx, та взявши до уваги гіпотезу плоских перерізів, розглянемо його деформований стан. Згадані перерізи повертаються один відносно одного на кут dθ, залишаючись при цьому пласкими. Елемент нейтрального шару між перерізами перетворюється на дугу з радіусом ρ, а волокно, розташоване на відстані z від нейтрального шару — на криволінійне волокно радіусом кривини ρ + z. Відносне видовження цього волокна з врахуванням, що dx=ρdφ:
- .
Отже, геометрична сторона задачі вказує на лінійну залежність деформації від відстані волокна стосовно нейтральної осі.
На підставі вимірювань відстаней між аналогічними точками довільних двох перерізів можна виявити, що верхні поздовжні волокна балки вкорочуються, а нижні — подовжуються. Але можна знайти і такі волокна, довжина яких при згинанні залишається незмінною. Сукупність волокон, які не змінюють своєї довжини при згинанні балки, називається нейтральним шаром. Волокна, що належать нейтральному шару до деформації лежать в одній площині, а в деформованому стані утворюють деяку циліндричну поверхню. В обох випадках кожний поперечний переріз балки перетинається з нейтральним шаром по прямій, яка називається нейтральною лінією або нейтральною віссю, положення останньої по висоті перерізу поки невідоме. Якщо всі зовнішні сили, що діють на прямий брус (включаючи реакції опор), розташовані в площині згинання перпендикулярно до вигнутої осі бруса, то нейтральний шар збігається з осьовим шаром, а нейтральна вісь утворюється перетином цього шару з поперечним перерізом.
Фізичний аспект задачі
Щоб записати закон Гука, що виражає фізичний бік задачі, слід з'ясувати, у якому напруженому стані перебуває довільне волокно балки в проміжку між перерізами. Оскільки дотичних напружень немає, та припускається, що волокна не тиснуть одне на одне, то можна вважати, що волокно перебуває у лінійному напруженому стані. Тому закон Гука можна записати у виді:
- .
З останніх двох рівнянь випливає, що:
На основі умови рівноваги зовнішніх і внутрішніх силових факторів та з врахуванням записаних вище рівнянь:
- , або
- .
На основі останніх виразів можна знайти:
- .
Ця формула, яка вперше була отримана французьким вченим К. Нав'є, дає змогу визначити нормальні напруження при чистому згині балки в будь-якій точці її перерізу. Формула показує, що незалежно від форми та розмірів перерізу балки, напруження в точках нейтральної лінії завжди дорівнюють нулю. Величина нормального напруження σ лінійно зростає по мірі віддалення від нейтральної лінії. При цьому напруження будуть однаковими по ширині перерізу уздовж лінії, паралельної до нейтральної. Максимальні напруження мають місце у найвіддаленіших від нейтральної лінії волокнах. Якщо нейтральний шар між двома поперечними перерізами розташований поза брусом то усі волокна бруса між цими перетинами або розтягнуті, або стиснені (один з випадків у складному згинанні).
Усі отримані формули виведено для випадку чистого згинання прямого бруса. Для загального випадку згинання дія поперечних сил призводить до того, що гіпотеза плоских перерізів, на якій ґрунтується виведення формули Нав'є для обчислення нормальних напружень не виконується оскільки поперечні перерізи викривляються а поздовжні волокна взаємодіють між собою, отже перебувають не в лінійному а плоскому напруженому стані. Проте практика розрахунків показує, що і при поперечному згинанні балок і рам, коли діють не лише моменти, а і поперечні і поздовжні сили, формули можна використовувати і похибка буде незначною.
Див. також
Джерела
- Опір матеріалів. Підручник /Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Г. С. Писаренка — К.: Вища школа,1993. — 655 с. ISBN 5-11-004083-4
- Шваб'юк В. І. Опір матеріалів: навч. посіб. для студентів ВНЗ / В. І. Шваб'юк. — К.:НТУ «КПІ», 2009. — 380 с.
- Мильніков О. В. Опір матеріалів. Конспект лекцій / Олександр Володимирович Мильніков. — Тернопіль: Видавництво ТНТУ, 2010. — 257 с.