Обирання моделі
Обира́ння моде́лі (англ. model selection) — задача обирання статистичної моделі з множини моделей-кандидатів на заданих даних. В найпростіших випадках розглядають вже наявний набір даних. Проте до цієї задачі входить і планування таких експериментів, щоби збирані дані добре підходили для задачі обирання моделі. За заданих моделей-кандидатів подібної передбачувальної або пояснювальної сили найкращим вибором, швидше за все, буде найпростіша модель.
Конісі та Кітагава, (2008, с. 75) заявляють, що «Більшість задач у статистичному висновуванні можна розглядати як задачі, пов'язані зі статистичним моделюванням». Пов'язано з цим, Кокс, (2006, с. 197) сказав: «Як здійснюється перенесення з моделі предметної області на статистичну модель, часто є найкритичнішою частиною аналізу». Вибір моделі може також стосуватися завдання вибору кількох моделей з великого набору обчислювальних моделей з метою прийняття рішення або оптимізації в умовах невизначеності.
Введення
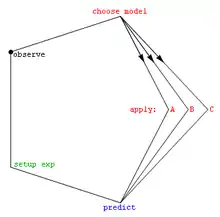
У своєму найпростішому вигляді, обирання моделі є однією з основних задач наукового дослідження. Визначення принципу, який пояснює ряд спостережень, часто безпосередньо пов'язано з математичною моделлю, що передбачує ці спостереження. Наприклад, коли Галілей виконував свої експерименти з похилою площиною, він показував, що рух куль відповідав параболі, передбаченій його моделлю.
Як хоча би почати обирати найкращу модель з незліченного числа можливих механізмів та процесів, що могли породити дані? Загальний математичний підхід полягає у виборі моделі серед множини кандидатів; цю множину мусить обрати дослідник. Часто використовують прості моделі, такі як поліноміальні, принаймні спочатку. Бернем та Андерсон, (2002) у своїй книзі підкреслюють важливість обирання моделі на основі правильних математичних принципів, таких як розуміння феноменологічних процесів або механізмів (наприклад, хімічних реакцій), що лежать в основі даних.
Щойно обрано множину моделей-кандидатів, статистичний аналіз дає нам можливість обирати найкращу з них. Розуміння того, що таке найкраща, є спірним. Добра методика обирання моделі балансуватиме між допасованістю та простотою. Складніші моделі матимуть кращу здатність допасовувати свою форму до даних (наприклад, многочлен п'ятого степеня може точно допасуватися до шести точок), але ці додаткові параметри можуть не представляти нічого корисного. (Можливо, ці шість точок насправді просто випадково розкидано по прямій ліній.) Допасованість, як правило, визначають застосуванням підходу відношення правдоподібностей, або його наближення, що веде до критерію хі-квадрат. Складність, як правило, вимірюють шляхом підрахунку числа параметрів моделі.
Методики обирання моделі можна розглядати як оцінки деякої фізичної величини, такої як ймовірність моделі, що виробляє задані дані. Важливими мірами якості цієї оцінки є як зсув, так і дисперсія, також розглядають й ефективність.
Стандартним прикладом обирання моделі є допасовування кривої, в якому для заданої множини точок та інших знань про обстановку (наприклад, що точки є результатом НОР-вибірки) ми мусимо обирати криву, яка описує функцію, що породила ці точки.
Методи обирання множини моделей-кандидатів
Критерії для обирання моделі
- Баєсів інформаційний критерій
- Інформаційний критерій Акаіке
- Інформаційний критерій девіантності
- Коефіцієнт Баєса
- Алгоритмічна теорія інформації
- Мінімізація структурного ризику
- Перевірка відношенням правдоподібностей - статистичний тест, що використовується для перевірки обмежень параметрів статистичних моделей, оцінених на основі вибіркових даних.
- Перехресне затверджування
- Покрокова регресія
- Рівень хибного виявляння
- Cp Меллоуза
- Сфокусований інформаційний критерій - критерій вибору статистичних моделей щодо їх ефективності для заданого параметра
- Інформаційний критерій Ватанабе-Акаяке - інформаційний критерій широкого застосування
Найширше вживаними критеріями є (i) інформаційний критерій Акаіке та (ii) коефіцієнт Баєса та/або баєсів інформаційний критерій (який до певної міри наближує коефіцієнт Баєса).
Див. також
- Аналіз ідентифіковності
- Всі моделі є неправильними
- Ґратковий пошук
- Дилема зсуву-дисперсії
- Задача ідентифікування параметрів
- Ідентифікування моделі
- Лезо Оккама
- Логарифмічно-лінійний аналіз
- Наукове моделювання
- Оптимальний план експерименту
- Оптимізація гіперпараметрів
- Парадокс Фрідмана
- Перевірка регресійних моделей
- Парадокс Штайна
Джерела
- Aho, K.; Derryberry, D.; Peterson, T. (2014). Model selection for ecologists: the worldviews of AIC and BIC. Ecology 95: 631–636. doi:10.1890/13-1452.1.. (англ.)
- Anderson, D.R. (2008). Model Based Inference in the Life Sciences. Springer. (англ.)
- Ando, T. (2010). Bayesian Model Selection and Statistical Modeling. CRC Press. (англ.)
- Breiman, L. (2001). Statistical modeling: the two cultures. Statistical Science 16: 199–231. doi:10.1214/ss/1009213726. (англ.)
- Burnham, K.P.; Anderson, D.R. (2002). Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach (вид. 2nd). Springer-Verlag. ISBN 0-387-95364-7. (англ.) [Це має понад 31000 цитувань на Google Scholar.]
- Chamberlin, T.C. (1890). The method of multiple working hypotheses. Science 15: 93. (передруковано 1965, Science 148: 754–759 .) (англ.)
- Claeskens, G. (2016). Statistical model choice. Annual Review of Statistics and Its Application 3: 233–256. doi:10.1146/annurev-statistics-041715-033413.[недоступне посилання з квітня 2019]. (англ.)
- Claeskens, G.; Hjort, N.L. (2008). Model Selection and Model Averaging. Cambridge University Press. (англ.)
- Cox, D.R. (2006). Principles of Statistical Inference. Cambridge University Press. (англ.)
- Konishi, S.; Kitagawa, G. (2008). Information Criteria and Statistical Modeling. Springer.. (англ.)
- Lahiri, P. (2001). Model Selection. Institute of Mathematical Statistics. (англ.)
- Leeb, H.; Pötscher, B. M. (2009). Model selection. У Anderson, T. G. Handbook of Financial Time Series. Springer. с. 889–925. doi:10.1007/978-3-540-71297-8_39. (англ.)
- Lukacs, P. M.; Thompson, W. L.; Kendall, W. L.; Gould, W. R.; Doherty, P. F. Jr.; Burnham, K. P.; Anderson, D. R. (2007). Concerns regarding a call for pluralism of information theory and hypothesis testing. Journal of Applied Ecology 44 (2): 456–460. doi:10.1111/j.1365-2664.2006.01267.x.. (англ.)
- Massart, P. (2007). Concentration Inequalities and Model Selection. Springer. (англ.)
- Shmueli, G. (2010). To explain or to predict?. Statistical Science 25: 289-310. MR MR2791669. doi:10.1214/10-STS330.. (англ.)
- Wit, E.; van den Heuvel, E.; Romeijn, J.-W. (2012). ‘All models are wrong...’: an introduction to model uncertainty. Statistica Neerlandica 66: 217–236. doi:10.1111/j.1467-9574.2012.00530.x.. (англ.)
