Однозв'язна область

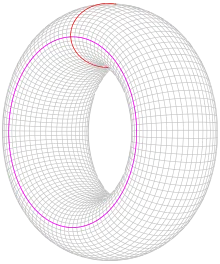
Однозв'язна область — топологічне поняття, що інтуїтивно позначає частину D лінійно зв'язного топологічного простору, в якій будь-який замкнутий шлях можна неперервно стягнути в точку, не виходячи за межі області D (область без «дірок»). Приклад: сфера однозв'язна, а поверхня тора не однозв'язна, тому що кола на ній, показані червоним на малюнку, не можна стягнути в точку. Поняття однозв'язності широко застосуванняовується в різних галузях математики, особливо в комплексному аналізі.

Стягнення контуру в точку на сфері

Поверхня тора — приклад неоднозв'язної області.

Означення

Область D лінійно зв'язного топологічного простору називається однозв'язною, якщо всі контури в ній гомотопні нулю. Еквівалентне означення: фундаментальна група для D тривіальна. Область, яка не є однозв'язною, називається багатозв'язною.

Еквівалентно лінійно зв'язна область X називається однозв'язною якщо для кожного неперервного відображення f : S¹ → X (де S¹ позначає одиничне коло) існує неперервне відображення F : D² → X (де D² позначає одиничний диск), таке що обмеження F на S¹ рівне f.

Приклади

Довільна опукла множина в евклідовому просторі однозв'язна.

Кругове кільце, стрічка Мебіуса, проективна площина не є однозв'язними.

Властивості

Однозв'язність є гомотопічним інваріантом, тобто гомотопічно еквівалентні простори або обидва є однозв'язними, або обидва не є однозв'язними.
Властивість однозв'язності не зберігається неперервними відображеннями. Наприклад образом комплексної площини (однозв'язна область) щодо експоненційної функції є комплексна площина без початку координат (що не є однозв'язною областю).

Література

Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
Келли Дж. Л. Общая топология — М.: Наука, 1968

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.