Окільцьований простір
Окільцьований простір — топологічний простір, кожній відкритій множині якого співставлено комутативне кільце «функцій» на цій множині. Окільцьовані простори, зокрема, використовуються при визначенні схем.
Визначення
Окільцьований простір — це топологічний простір разом з пучком комутативний кілець на ньому. Цей пучок називається структурним пучком простору .
Локально окільцьований простір — це окільцьований простір, такий що шар пучка в будь-якій точці — є локальним кільцем.
Приклади
Будь-який топологічний простір можна наділити структурою локально окільцьованого простору, якщо розглянути пучок неперервних функцій на ньому. Шар цього пучка в точці x — кільце ростків неперервних функцій в x є локальним кільцем, єдиний максимальний ідеал якого — паростки функцій, рівних нулю в x. Аналогічним чином, гладкий многовид з пучком гладких функцій є локально окільцьованим простором.
ЯкщоX — алгебраїчний многовид з топологією Зариського (наприклад, спектр деякого кільця), структуру локально окільцьованого простору на ньому вводять в такий спосіб: — множина раціональних функцій, визначених на всьому U. Такий окільцьований простір називають афінною схемою, загальні схеми визначають як результат «склеювання» кількох афінних схем.
Морфізми окільцьованих просторів
Для того, щоб задати морфізм з в , потрібно зафіксувати наступну інформацію:
- Неперервне відображення .
- Для кожної відкритої підмножини — гомоморфізм кілець .
Гомоморфізми кілець повинні бути узгоджені зі структурою пучка, тобто комутувати з відображеннями обмеження. А саме, якщо — відкриті підмножини , наступна діаграма повинна бути комутативною:
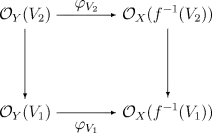
Морфізми локально окільцьованих просторів повинні задовольняти ще одній вимозі. Гомоморфізми для кожної точки індукують гомоморфізм з шару в точці в шар в точці . Потрібно, щоб всі ці гомоморфізми були локальними, тобто переводили максимальний ідеал прообразу в підмножину максимального ідеалу образу.
Дотичний простір
Структура локально окільцьованих просторів дозволяє ввести осмислене визначення дотичного простору в його точці. Розглянемо точку окільцьованого простору . Розглянемо локальне кільце (шар пучка в точці x) з максимальним ідеалом . Тоді — поле, — векторний простір над цим полем. Дотичний простір в точці визначається як двоїстий простір до цього простору.
Ідея полягає в наступному: дотичний простір складається з векторів, уздовж яких можна «диференціювати» «функції» в даній точці, тобто елементи кільця . Досить знайти спосіб диференціювання функцій, значення яких в даній точці дорівнює нулю, так як інші відрізняються від них на константу, то є достатньо описати похідні функцій з . При цьому диференціал добутку двох функцій з дорівнює нулю (ми хочемо, щоб формула похідної добутку залишилася вірною). Отже, вектор повинен привласнювати число кожного елементу , і це те, що роблять елементи двоїстого простору.
Легко перевірити, що в разі гладких многовидів з пучком гладких функцій це визначення збігається зі звичайним. З іншого боку, в разі топологічного простору з пучком неперервних (дійснозначних) функцій , так як для неперервної функції функція також є неперервною. Отже, в цьому випадку дотичний простір в будь-якій точці має розмірність 0.
Посилання
- Onishchik, A.L. (2001). Ringed space. У Hazewinkel, Michiel. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.
Джерела
- Tennison, B. R. (1975). Sheaf theory. Cambridge University Press. MR 0404390.