Пучок (математика)

На топологічному просторі X заданий передпучок ${\displaystyle {\mathcal {F}}}$ об'єктів, якщо:

• Кожній відкритій підмножині ${\displaystyle U\subset X}$ зіставлений певний об'єкт деякої категорії ${\displaystyle {\mathcal {C}}}$ (найчастіше деяка множина, абелева група, кільце, модуль над кільцем і т. п.) ${\displaystyle {\mathcal {F}}(U)\in {\mathcal {C}}}$.
• Для кожної пари відкритих множин ${\displaystyle V\subset U}$ визначений морфізм обмеження ${\displaystyle \rho _{VU}:{\mathcal {F}}(U)\rightarrow {\mathcal {F}}(V)}$ такий, що ${\displaystyle \rho _{UU}}$ — тотожний морфізм об'єкта ${\displaystyle {\mathcal {F}}(U)}$ і для кожної трійки відкритих множин ${\displaystyle W\subset V\subset U}$ виконується:

${\displaystyle \rho _{WU}=\rho _{WV}\circ \rho _{VU}}$

Якщо об'єкти ${\displaystyle {\mathcal {C}}}$ є множинами, то елементи ${\displaystyle {\mathcal {F}}(U)}$ називаються перерізами пучка над множиною U.

Іншими словами, передпучок — контраваріантний функтор з категорії відкритих підмножин X і їх вкладень в деяку категорію.

Передпучок ${\displaystyle {\mathcal {F}}}$ на X називається пучком (множин, абелевих груп, кілець, модулів над кільцем і т. п.) якщо для довільної відкритої множини V простору X, її відкритого покриття сімейством відкритих множин ${\displaystyle \{V_{i}\}_{I}}$, і для довільних перерізів ${\displaystyle \{s_{i}\}_{I}}$ передпучка ${\displaystyle {\mathcal {F}}}$ над множинами ${\displaystyle V_{i}}$, з того що :

${\displaystyle s_{i}|_{V_{i}\cap V_{j}}=s_{j}|_{V_{i}\cap V_{j}}}$

випливає існування єдиного перерізу s передпучка ${\displaystyle {\mathcal {F}}}$ над V такого що : ${\displaystyle s|_{V_{i}}=s_{i}}$.

Замітка. Визначення пучка існує і у випадку коли об'єктами категорії не є множини. Проте цей випадок вимагає глибших понять теорії категорій і не часто використовується у застосуваннях.

Одним з найпростіших і найважливіших прикладів є пучок неперервних функцій на топологічному просторі X. Обмеження неперервної функції на відкриту підмножину є неперервною функцією на цій підмножині, і функція, задана частково на відкритих підмножинах, може бути відновлена на їх об'єднанні.

Точніше, для кожної відкритої підмножини U простору X позначимо F(U) множину всіх неперервних дійснозначних функцій ${\displaystyle f:X\to \mathbb {R} }$. Маючи відкриту множину V, що міститься в U, і функції f з F(U), ми можемо звузити область визначення функції f до множини V і одержати функцію ${\displaystyle f|_{V}}$. Обмеження ${\displaystyle f|_{V}}$ є неперервною функцією на V, отже, воно є елементом множини F(V). Таким чином, визначено відображення обмеження ${\displaystyle \rho _{VU}:F(U)\to F(V)}$.

Припустимо, що задана узгоджена система неперервних функцій ${\displaystyle f_{i}:U_{i}\to \mathbb {R} ,i\in I}$. Це означає, що обмеження функцій f_i і f_j на множині ${\displaystyle U_{i}\cap U_{j}}$ повинні бути рівними. Визначимо тепер функцію ${\displaystyle f:U\to \mathbb {R} }$ таким чином: оскільки U - об'єднання всіх U_i, кожна точка x з U покрита множиною U_i для деякого i. Визначимо значення функції f в точці x рівним f_i(x). Це визначення коректно: якщо x лежить також і в U_j, то по умові узгодженості f_i(x)= f_j(x), тому все одно, яку з цих функцій користуватися для визначення f(x). При цьому функція f неперервна в точці x, оскільки в її околі U_i вона рівна неперервній функції f_i(x). У результаті функція f неперервна в кожній точці з U, тобто неперервна в U. Більш того, f — єдина неперервна функція, обмеження якої на області U_i рівне f_i, оскільки функція повністю визначається своїми значеннями в точках.

Насправді, одержаний пучок є не просто пучком множин. Оскільки неперервні функції можна поточково додавати і одержувати знову неперервні функції, цей пучок також є пучком абелевих груп. Оскільки їх також можна перемножувати, цей пучок є пучком комутативних кілець. Оскільки неперервні функції на множині утворюють векторний простір над ${\displaystyle \mathbb {R} }$, то цей пучок — пучок алгебр над ${\displaystyle \mathbb {R} }$.

У цьому розділі всі пучки визначені над простором X і приймають значення у фіксованій категорії C (коли мова піде про ядро і коядро морфізмів, передбачається, що C — абелева категорія).

Нехай ${\displaystyle {\mathcal {F}}}$ і ${\displaystyle {\mathcal {G}}}$ — два такі пучки. Морфізм C-пучків на X ${\displaystyle \varphi \colon {\mathcal {G}}\to {\mathcal {F}}}$ зіставляє кожній відкритій множині U простори X морфізм ${\displaystyle \varphi _{U}\colon {\mathcal {G}}(U)\to {\mathcal {F}}(U),}$ так що всі ці морфізми узгоджено один з одним і відображеннями обмеження в обох пучках. Іншими словами, для кожної відкритої підмножини U і відкритої множини V має місце комутативна діаграма:

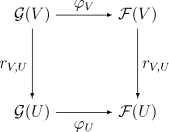
Ця умова узгодженості означає, що кожному перетину s пучка F над відкритою множиною U зіставлено деякий переріз ${\displaystyle \varphi _{U}(s)}$ над U пучка G, і їх обмеження на відкриту підмножину V безлічі U зв'язані морфізмом ${\displaystyle \varphi _{V}}$. (Обмеження на V ${\displaystyle \varphi _{U}}$-образа перерізу s рівне ${\displaystyle \varphi _{V}}$-образу його обмеження на V.)

Простий факт, що морфізм пучків є ізоморфізмом (тобто має обернений морфізм) тоді і тільки тоді, коли всі морфізми ${\displaystyle \varphi _{U}}$ є ізоморфізмами. Те ж вірно для мономорфізмів і не вірно для епіморфізмів. Це пов'язано з тим, що ядро морфізму пучків завжди є пучком, а образ і коядро можуть і не бути.

Далі пучки приймають значення у фіксованій категорії C, але можуть бути визначені над різними просторами.

Нехай X і Y — топологічні простори із заданими на них пучками O_X і O_Y відповідно. Морфізм пари (X, O_X) в (Y, O_Y) задається за допомогою наступних даних:

• Неперервне відображення f : X → Y
• сімейство C-морфізмів φ_V : O_Y(V)→ O_X(f ^-1(V)) для кожної відкритої підмножини V простору Y, які комутують з відображеннями обмеження. Тобто, якщо V₁ ⊂ V₂ - дві відкриті підмножини Y, наступна діаграма повинна бути комутативною (вертикальні стрілки — морфізми обмеження на підмножину):

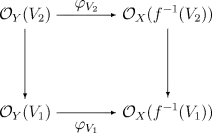
Це визначення годиться і для визначення морфізму передпучків над різними просторами.