Оптичний потік
Опти́чний поті́к (англ. optical flow, optic flow) — це схема видимого руху об'єктів, поверхонь і граней у зоровій сцені, спричинюваного відносним рухом спостерігача та сцени.[1][2] Оптичний потік також можливо визначити як розподіл видимих швидкостей руху візерунку яскравості в зображенні.[3] Поняття оптичного потоку було запроваджено американським психологом Джеймсом Дж. Ґібсоном у 1940-х роках для опису зорових стимулів, що виникають у тварин, які рухаються світом.[4] Джеймс Ґібсон наголосив на важливості оптичного потоку для сприймання можливостей, здатності розрізнювати можливості для дій у середовищі. Послідовники Ґібсона та його екологічного підходу до психології згодом показати роль стимулу оптичного потоку для сприймання руху спостерігачем у світі; сприймання форми, відстані й руху об'єктів у світі; та контролю пересування.[5]
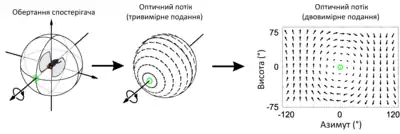
Термін «оптичний потік» також використовують робототехніки, охоплюючи споріднені методики з обробки зображень та керування навігацією, включно з виявлянням руху, сегментуванням об'єктів, інформацією про час до контакту, обчисленнями фокусу розширення, освітленістю, кодуванням компенсації руху, та вимірюванням стереодиспаритету.[6][7]
Оцінювання
Послідовності впорядкованих зображень уможливлюють оцінювання руху або як миттєвих швидкостей зображення, або як дискретних зміщень зображень.[7] Фліт та Вейсс пропонують навчальний посібник з оптичного потоку на основі градієнта.[8] Джон Л. Баррон, Девід Дж. Фліт та Стівен Бошемен пропонують аналіз продуктивності низки методик оптичного потоку, з наголосом на точності та густоті вимірювань.[9]
Методи оптичного потоку намагаються обчислювати рух між двома кадрами, що було знято в моменти часу та , в положенні кожного вокселя. Ці методи називають диференціальними, оскільки вони ґрунтуються на локальних наближеннях сигналу зображення рядами Тейлора, тобто, вони використовують частинні похідні за просторовими та часовими координатами.
Для (2D + t)-вимірного випадку (випадки 3D та n-D є подібними) воксель у положенні з інтенсивністю буде переміщено між цими двома кадрами на , та , й може бути задано наступне обмеження сталості яскравості (англ. brightness constancy constraint):
Якщо виходити з того, що переміщення є невеликим, це обмеження зображення в може бути розгорнуло за допомогою ряду Тейлора в
- члени вищих порядків
При відкиданні членів вищих порядків (що здійснює лінеаризацію) з цього випливає, що
або, при діленні на ,
що в результаті дає
де є складовими та швидкості або оптичного потоку , а , та є похідними зображення в у відповідних напрямках. Далі ці похідні може бути позначено через , та .
Отже:
або
Це — рівняння з двома невідомими, й саме по собі розв'язаним бути не може. Це відоме як проблема вікна (англ. aperture problem) в алгоритмах оптичного потоку. Щоби знайти оптичний потік, потрібен інший набір рівнянь, заданий деяким додатковим обмеженням. Для оцінювання фактичного потоку всі алгоритми оптичного потоку запроваджують додаткові умови.
Методи визначення
- Фазова кореляція — обернення унормованого спектру взаємної потужності
- Блокові методи — мінімізування суми квадратів різниць, або суми модулів різниць, або максимізування унормованої взаємної кореляції
- Диференціальні методи оцінювання оптичного потоку, що ґрунтуються на частинних похідних сигналу зображення та/або шуканого поля потоку та частинних похідних вищого порядку, такі як:
- Метод Лукаса — Канаде — стосовно клаптиків зображення та афінної моделі для поля потоку[10]
- Метод Горна — Шунка — оптимізування функціоналу на основі залишків від обмеження сталості яскравості, та певного члена регуляризації, що виражає очікувану плавність поля потоку[10]
- Метод Бакстона — Бакстона — ґрунтується на моделі руху контурів у послідовностях зображень[11]
- Метод Блека — Джепсона — грубий оптичний потік через кореляцію[7]
- Загальні варіаційні методи — низка видозмін/розширень Горна — Шунка, що використовують інші члени даних, та інші члени гладкості.
- Дискретні методи оптимізації — простір пошуку дискретизується, й узгодження зображення відтак обробляється через призначування міток на кожному пікселі таким чином, що відповідне деформування мінімізує відстань між первинним та цільовим зображеннями.[12] Оптимальний розв'язок часто добувають через алгоритми теореми про максимальний потік, мінімальний розріз, лінійне програмування, або методи поширення переконання.
Багато з них, на додачу до поточних алгоритмів на рівні останніх досягнень, оцінюють на наборі даних Middlebury Benchmark Dataset.[13][14] Іншими популярними наборами даних є KITTI та Sintel.
Використання
Головними аспектами дослідження оптичного потоку стали оцінювання руху та стискання відео. Хоча поле оптичного потоку на перший погляд і схоже на щільне поле руху, отримуване за допомогою методик оцінювання руху, оптичний потік є дослідженням не лише визначення самого поля оптичного потоку, але також і його використання в оцінюванні тривимірної природи та структури сцени, як і тривимірного руху об'єктів та спостерігача відносно сцени, де здебільшого використовують якобіан зображення.[15]
Дослідники в галузі робототехніки використовували оптичний потік в багатьох областях, таких як виявляння та відстежування об'єктів, виділяння основного плану зображення, виявляння руху, навігація роботів та візуальна одометрія.[6] Інформацію оптичного потоку визнавали корисною для керування мініатюрними літальними апаратами.[16]
До застосувань оптичного потоку належить задача висновування не лише руху спостерігача та об'єктів у сцені, але також і структури об'єктів та середовища. Оскільки усвідомлення руху та породжування ментальних мап структури нашого середовища є критичними складовими тваринного (та людського) зору, перетворення цієї вродженої здібності на комп'ютерну здатність є так само вирішальним й у галузі зору машинного.[17]
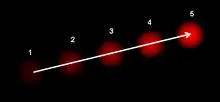
Розгляньмо п'ятикадровий кліп руху м'яча з лівої нижньої частини поля зору до правої верхньої. Методики оцінювання руху можуть визначити, що на двовимірній площині м'яч рухається вгору та праворуч, й вектори, що описують цей рух, можливо виділити з цієї послідовності кадрів. Для цілей стискання відео (наприклад, MPEG), послідовність тепер описано настільки добре, наскільки потрібно. Проте в галузі машинного зору питання про те, чи це м'яч рухається праворуч, чи спостерігач рухається ліворуч, є непізнанною, але критичною інформацією. Навіть якби в цих п'яти кадрах було присутнє статичне візерункове тло, ми не змогли би з упевненістю стверджувати, що м'яч рухався праворуч, оскільки цей візерунок міг мати нескінченну відстань від спостерігача.
Давач оптичного потоку
Давач оптичного потоку — це зоровий давач, здатний вимірювати оптичний потік або візуальний рух, та видавати вимірювання, що ґрунтуються на оптичному потоці. Існують різноманітні конфігурації давачів оптичного потоку. Однією з конфігурацій є чип давача зображення, з'єднаний з процесором, запрограмованим виконувати алгоритм оптичного потоку. Інша конфігурація використовує зоровий чип, що є інтегрованою схемою, яка має як давач зображення, так і процесор, на одному й тому ж кристалі, що уможливлює компактне втілення.[18][19] Таким прикладом є звичайний давач оптичної миші. У деяких випадках схему обробки може бути втілено із застосуванням схем з аналоговим або змішаними сигналами для уможливлення швидкого обчислювання оптичного потоку з мінімальним споживанням струму.
Однією з областей сучасних досліджень є застосування методик нейроморфної інженерії для втілення схем, що реагують на оптичний потік, і відтак можуть бути доречними для використання в давачі оптичного потоку.[20] Такі схеми можуть черпати натхнення з біологічних нейронних схем, що реагують на оптичний потік подібним чином.
Давачі оптичного потоку широко використовують у комп'ютерних оптичних мишах як головну давачеву складову для вимірювання руху миші поверхнею.
Давачі оптичного потоку використовують також і в робототехніці, переважно де є потреба у вимірюванні візуального руху або відносного руху робота та інших об'єктів поблизу робота. Однією з областей поточних досліджень також є використання давачів оптичного потоку в безпілотних літальних апаратах (БПЛА) задля забезпечення стабільності та уникання перешкод.[21]
Див. також
- Осяжний оптичний лад
- Оптична миша
- Дальнісне зображення
- Зоровий процесор
- Рівняння неперервності
Примітки
- Burton, Andrew; Radford, John (1978). Thinking in Perspective: Critical Essays in the Study of Thought Processes. Routledge. ISBN 978-0-416-85840-2. (англ.)
- Warren, David H.; Strelow, Edward R. (1985). Electronic Spatial Sensing for the Blind: Contributions from Perception. Springer. ISBN 978-90-247-2689-9. (англ.)
- Horn, Berthold K.P.; Schunck, Brian G. (August 1981). Determining optical flow. Artificial Intelligence (англ.) 17 (1–3): 185–203. doi:10.1016/0004-3702(81)90024-2. Проігноровано невідомий параметр
|hdl=(довідка) (англ.) - Gibson, J.J. (1950). The Perception of the Visual World. Houghton Mifflin. (англ.)
- Royden, C. S.; Moore, K. D. (2012). Use of speed cues in the detection of moving objects by moving observers. Vision Research 59: 17–24. PMID 22406544. doi:10.1016/j.visres.2012.02.006. Проігноровано невідомий параметр
|s2cid=(довідка) (англ.) - Aires, Kelson R. T.; Santana, Andre M.; Medeiros, Adelardo A. D. (2008). Optical Flow Using Color Information. ACM New York, NY, USA. ISBN 978-1-59593-753-7. (англ.)
- Beauchemin, S. S.; Barron, J. L. (1995). The computation of optical flow. ACM Computing Surveys (ACM New York, USA) 27 (3): 433–466. doi:10.1145/212094.212141. Проігноровано невідомий параметр
|s2cid=(довідка) (англ.) - Fleet, David J.; Weiss, Yair (2006). Optical Flow Estimation. У Paragios, Nikos; Chen, Yunmei; Faugeras, Olivier D. Handbook of Mathematical Models in Computer Vision. Springer. с. 237–257. ISBN 978-0-387-26371-7. (англ.)
- Barron, John L.; Fleet, David J.; Beauchemin, Steven (1994). Performance of optical flow techniques. International Journal of Computer Vision 12: 43–77. doi:10.1007/bf01420984. Проігноровано невідомий параметр
|name-list-style=(довідка); Проігноровано невідомий параметр|s2cid=(довідка); Проігноровано невідомий параметр|citeseerx=(довідка) (англ.) - Zhang, G.; Chanson, H. (2018). Application of Local Optical Flow Methods to High-Velocity Free-surface Flows: Validation and Application to Stepped Chutes. Experimental Thermal and Fluid Science 90: 186–199. doi:10.1016/j.expthermflusci.2017.09.010. (англ.)
- Glyn W. Humphreys and Vicki Bruce (1989). Visual Cognition. Psychology Press. ISBN 978-0-86377-124-8. (англ.)
- B. Glocker; N. Komodakis; G. Tziritas; N. Navab; N. Paragios (2008). Dense Image Registration through MRFs and Efficient Linear Programming. Medical Image Analysis Journal. (англ.)
- Baker, Simon; Scharstein, Daniel; Lewis, J. P.; Roth, Stefan; Black, Michael J.; Szeliski, Richard (March 2011). A Database and Evaluation Methodology for Optical Flow. International Journal of Computer Vision (англ.) 92 (1): 1–31. ISSN 0920-5691. doi:10.1007/s11263-010-0390-2. Проігноровано невідомий параметр
|s2cid=(довідка) (англ.) - Baker, Simon; Scharstein, Daniel; Lewis, J. P.; Roth, Stefan; Black, Michael J.; Szeliski, Richard. Optical Flow. vision.middlebury.edu. Процитовано 18 жовтня 2019. (англ.)
- Corke, Peter (8 травня 2017). The Image Jacobian. QUT Robot Academy. (англ.)
- Barrows, G. L.; Chahl, J. S.; Srinivasan, M. V. (2003). Biologically inspired visual sensing and flight control. Aeronautical Journal 107 (1069): 159–268. doi:10.1017/S0001924000011891 — через Cambridge University Press. Проігноровано невідомий параметр
|doi-broken-date=(довідка) (англ.) - Brown, Christopher M. (1987). Advances in Computer Vision. Lawrence Erlbaum Associates. ISBN 978-0-89859-648-9. (англ.)
- Moini, Alireza (2000). Vision Chips. Boston, MA: Springer US. ISBN 9781461552673. OCLC 851803922. (англ.)
- Mead, Carver (1989). Analog VLSI and neural systems. Reading, Mass.: Addison-Wesley. ISBN 0201059924. OCLC 17954003. (англ.)
- Stocker, Alan A. (2006). Analog VLSI circuits for the perception of visual motion. Chichester, England: John Wiley & Sons. ISBN 0470034882. OCLC 71521689. (англ.)
- Floreano, Dario; Zufferey, Jean-Christophe; Srinivasan, Mandyam V. та ін., ред. (2009). Flying insects and robots. Heidelberg: Springer. ISBN 9783540893936. OCLC 495477442. (англ.)
Посилання
- Finding Optic Flow (англ.)
- Стаття Art of Optical Flow на fxguide.com (з використанням оптичного потоку у візуальних ефектах) (англ.)
- Optical flow evaluation and ground truth sequences. (англ.)
- Middlebury Optical flow evaluation and ground truth sequences. (англ.)
- mrf-registration.net — оцінювання оптичного потоку за допомогою МВП (англ.)
- The French Aerospace Lab: втілення оптичного потоку на основі Лукаса — Канаде на ГП (англ.)
- Втілення на CUDA від CUVI (CUDA Vision & Imaging Library) (англ.)
- Horn and Schunck Optical Flow: інтерактивне демо та первинний код методу Горна та Шунка
- TV-L1 Optical Flow: інтерактивне демо та первинний код методу Зака та ін.
- Robust Optical Flow: інтерактивне демо та первинний код методу Брокса та ін.
