Поліноми Лежандра

Поліноми Лежандра — ортогональні поліноми на інтервалі ${\displaystyle [-1,1]}$.

Ортогональні поліноми
Лежандра
Відкриті	Адрієн-Марі Лежандр
Формула	${\displaystyle P_{n}(x)={1 \over 2^{n}n!}{d^{n} \over dx^{n}}\left[(x^{2}-1)^{n}\right]}$
Диференціальне рівняння	${\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P_{n}(x)\right]+n(n+1)P_{n}(x)=0}$
Визначені на	${\displaystyle \ [-1,+1]}$
Вага	1
Норма	${\displaystyle {2 \over {2n+1}}}$
Примітки

Поліноми Лежандра можна отримати з системи поліномів ${\displaystyle 1,x,x^{2},x^{3},\ldots }$ за допомогою ортогоналізації Грама-Шмідта.

Можуть бути обчислені за допомогою прямих формул:

${\displaystyle P_{n}(x)={1 \over 2^{n}n!}{d^{n} \over dx^{n}}\left[(x^{2}-1)^{n}\right]}$

або за рекурентними:

${\displaystyle P_{n+1}(x)={2n+1 \over {n+1}}xP_{n}(x)-{n \over {n+1}}P_{n-1}(x).}$

Вони є розв'язками диференційного рівняння Лежандра:

${\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P_{n}(x)\right]+n(n+1)P_{n}(x)=0.}$

Графіки поліномів Лежандра порядку ${\displaystyle n=0,1,...,5}$

Генератриса для многочленів Лежандра дорівнює

${\displaystyle \sum _{n=0}^{\infty }P_{n}(z)x^{n}={1 \over {\sqrt {1-2xz+x^{2}}}}.}$

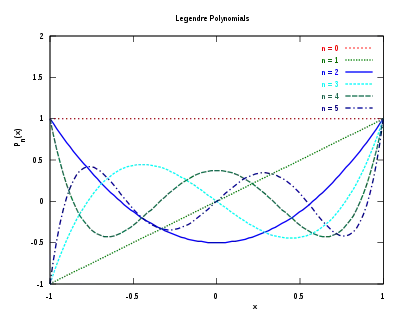
Перші 9 поліномів Лежандра:

${\displaystyle \ P_{0}(x)=1}$

${\displaystyle \ P_{1}(x)=x}$

${\displaystyle P_{2}(x)={\begin{matrix}{\frac {1}{2}}\end{matrix}}(3x^{2}-1)}$

${\displaystyle P_{3}(x)={\begin{matrix}{\frac {1}{2}}\end{matrix}}(5x^{3}-3x)}$

${\displaystyle P_{4}(x)={\begin{matrix}{\frac {1}{8}}\end{matrix}}(35x^{4}-30x^{2}+3)}$

${\displaystyle P_{5}(x)={\begin{matrix}{\frac {1}{8}}\end{matrix}}(63x^{5}-70x^{3}+15x)}$

${\displaystyle P_{6}(x)={\begin{matrix}{\frac {1}{16}}\end{matrix}}(231x^{6}-315x^{4}+105x^{2}-5)}$

${\displaystyle P_{7}(x)={\begin{matrix}{\frac {1}{16}}\end{matrix}}(429x^{7}-693x^{5}+315x^{3}-35x)}$

${\displaystyle P_{8}(x)={\begin{matrix}{\frac {1}{128}}\end{matrix}}(6435x^{8}-12012x^{6}+6930x^{4}-1260x^{2}+35)}$

${\displaystyle P_{9}(x)={\begin{matrix}{\frac {1}{128}}\end{matrix}}(12155x^{9}-25740x^{7}+18018x^{5}-4620x^{3}+315x)}$